Reflections from the 2024 Large Language Model (LLM) Hackathon for Applications in Materials Science and Chemistry

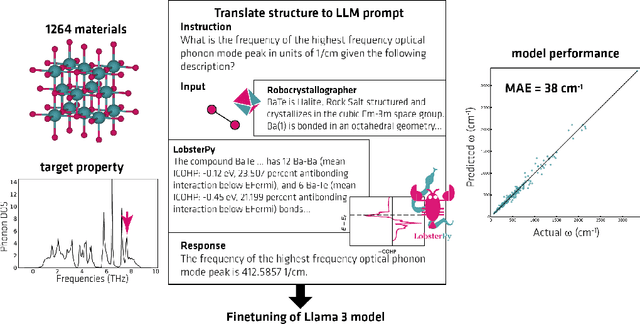
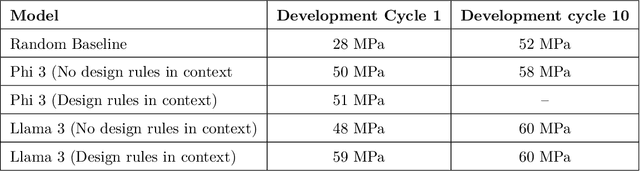
Here, we present the outcomes from the second Large Language Model (LLM) Hackathon for Applications in Materials Science and Chemistry, which engaged participants across global hybrid locations, resulting in 34 team submissions. The submissions spanned seven key application areas and demonstrated the diverse utility of LLMs for applications in (1) molecular and material property prediction; (2) molecular and material design; (3) automation and novel interfaces; (4) scientific communication and education; (5) research data management and automation; (6) hypothesis generation and evaluation; and (7) knowledge extraction and reasoning from scientific literature. Each team submission is presented in a summary table with links to the code and as brief papers in the appendix. Beyond team results, we discuss the hackathon event and its hybrid format, which included physical hubs in Toronto, Montreal, San Francisco, Berlin, Lausanne, and Tokyo, alongside a global online hub to enable local and virtual collaboration. Overall, the event highlighted significant improvements in LLM capabilities since the previous year's hackathon, suggesting continued expansion of LLMs for applications in materials science and chemistry research. These outcomes demonstrate the dual utility of LLMs as both multipurpose models for diverse machine learning tasks and platforms for rapid prototyping custom applications in scientific research.

In Context Learning and Reasoning for Symbolic Regression with Large Language Models

Large Language Models (LLMs) are transformer-based machine learning models that have shown remarkable performance in tasks for which they were not explicitly trained. Here, we explore the potential of LLMs to perform symbolic regression -- a machine-learning method for finding simple and accurate equations from datasets. We prompt GPT-4 to suggest expressions from data, which are then optimized and evaluated using external Python tools. These results are fed back to GPT-4, which proposes improved expressions while optimizing for complexity and loss. Using chain-of-thought prompting, we instruct GPT-4 to analyze the data, prior expressions, and the scientific context (expressed in natural language) for each problem before generating new expressions. We evaluated the workflow in rediscovery of five well-known scientific equations from experimental data, and on an additional dataset without a known equation. GPT-4 successfully rediscovered all five equations, and in general, performed better when prompted to use a scratchpad and consider scientific context. We also demonstrate how strategic prompting improves the model's performance and how the natural language interface simplifies integrating theory with data. Although this approach does not outperform established SR programs where target equations are more complex, LLMs can nonetheless iterate toward improved solutions while following instructions and incorporating scientific context in natural language.

Incorporating Background Knowledge in Symbolic Regression using a Computer Algebra System

Symbolic Regression (SR) can generate interpretable, concise expressions that fit a given dataset, allowing for more human understanding of the structure than black-box approaches. The addition of background knowledge (in the form of symbolic mathematical constraints) allows for the generation of expressions that are meaningful with respect to theory while also being consistent with data. We specifically examine the addition of constraints to traditional genetic algorithm (GA) based SR (PySR) as well as a Markov-chain Monte Carlo (MCMC) based Bayesian SR architecture (Bayesian Machine Scientist), and apply these to rediscovering adsorption equations from experimental, historical datasets. We find that, while hard constraints prevent GA and MCMC SR from searching, soft constraints can lead to improved performance both in terms of search effectiveness and model meaningfulness, with computational costs increasing by about an order-of-magnitude. If the constraints do not correlate well with the dataset or expected models, they can hinder the search of expressions. We find Bayesian SR is better these constraints (as the Bayesian prior) than by modifying the fitness function in the GA