PC-SRIF: Preconditioned Cholesky-based Square Root Information Filter for Vision-aided Inertial Navigation

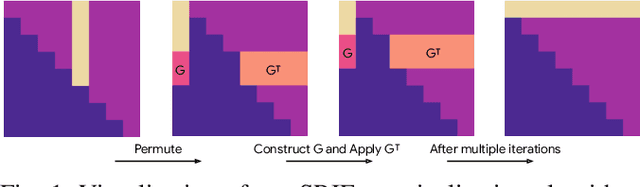
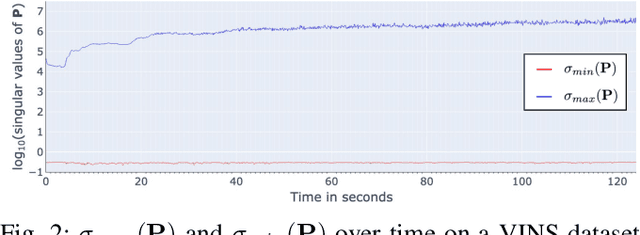
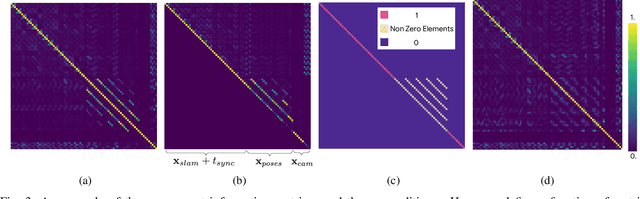
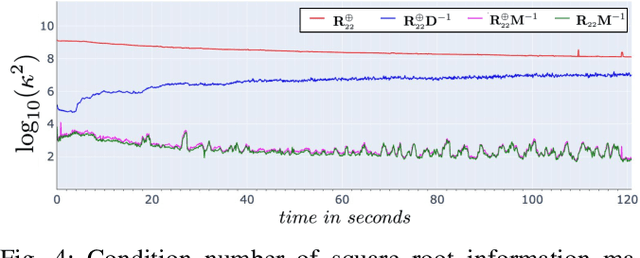
In this paper, we introduce a novel estimator for vision-aided inertial navigation systems (VINS), the Preconditioned Cholesky-based Square Root Information Filter (PC-SRIF). When solving linear systems, employing Cholesky decomposition offers superior efficiency but can compromise numerical stability. Due to this, existing VINS utilizing (Square Root) Information Filters often opt for QR decomposition on platforms where single precision is preferred, avoiding the numerical challenges associated with Cholesky decomposition. While these issues are often attributed to the ill-conditioned information matrix in VINS, our analysis reveals that this is not an inherent property of VINS but rather a consequence of specific parameterizations. We identify several factors that contribute to an ill-conditioned information matrix and propose a preconditioning technique to mitigate these conditioning issues. Building on this analysis, we present PC-SRIF, which exhibits remarkable stability in performing Cholesky decomposition in single precision when solving linear systems in VINS. Consequently, PC-SRIF achieves superior theoretical efficiency compared to alternative estimators. To validate the efficiency advantages and numerical stability of PC-SRIF based VINS, we have conducted well controlled experiments, which provide empirical evidence in support of our theoretical findings. Remarkably, in our VINS implementation, PC-SRIF's runtime is 41% faster than QR-based SRIF.

RISE-SLAM: A Resource-aware Inverse Schmidt Estimator for SLAM

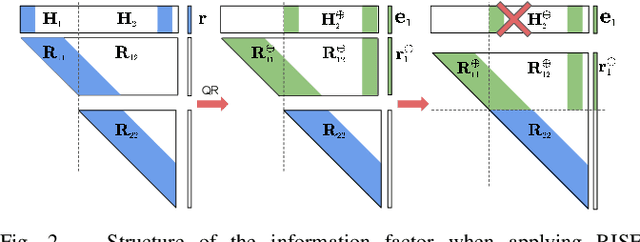
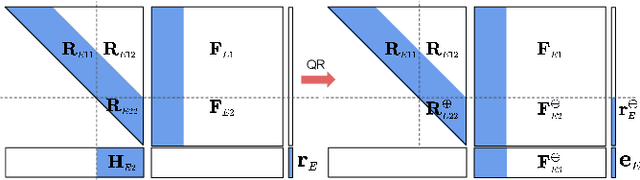
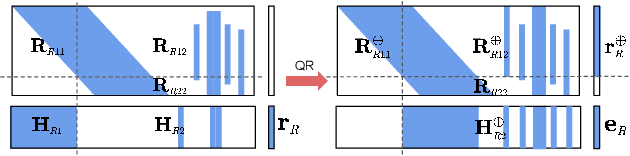
In this paper, we present the RISE-SLAM algorithm for performing visual-inertial simultaneous localization and mapping (SLAM), while improving estimation consistency. Specifically, in order to achieve real-time operation, existing approaches often assume previously-estimated states to be perfectly known, which leads to inconsistent estimates. Instead, based on the idea of the Schmidt-Kalman filter, which has processing cost linear in the size of the state vector but quadratic memory requirements, we derive a new consistent approximate method in the information domain, which has linear memory requirements and adjustable (constant to linear) processing cost. In particular, this method, the resource-aware inverse Schmidt estimator (RISE), allows trading estimation accuracy for computational efficiency. Furthermore, and in order to better address the requirements of a SLAM system during an exploration vs. a relocalization phase, we employ different configurations of RISE (in terms of the number and order of states updated) to maximize accuracy while preserving efficiency. Lastly, we evaluate the proposed RISE-SLAM algorithm on publicly-available datasets and demonstrate its superiority, both in terms of accuracy and efficiency, as compared to alternative visual-inertial SLAM systems.

Deep Multi-view Depth Estimation with Predicted Uncertainty

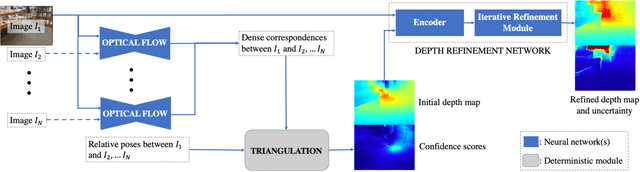
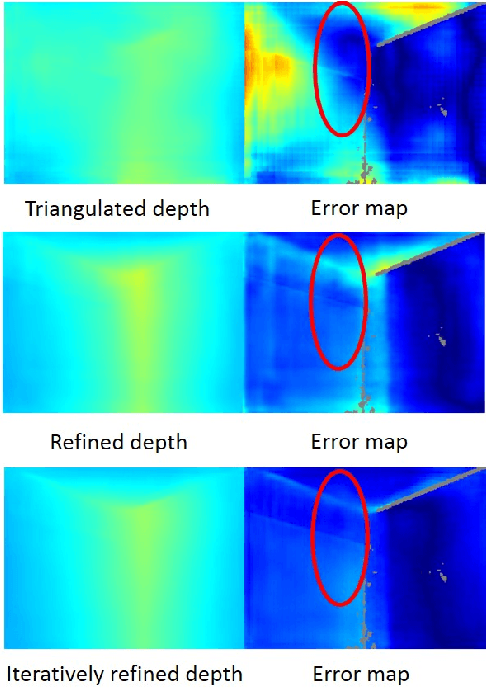
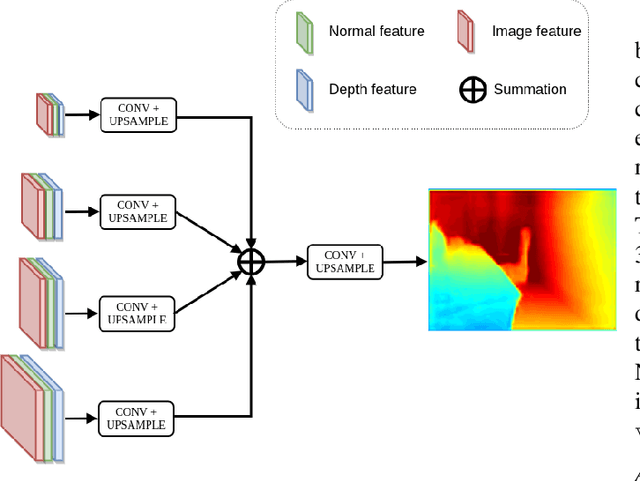
In this paper, we address the problem of estimating dense depth from a sequence of images using deep neural networks. Specifically, we employ a dense-optical-flow network to compute correspondences and then triangulate the point cloud to obtain an initial depth map. Parts of the point cloud, however, may be less accurate than others due to lack of common observations or small baseline-to-depth ratio. To further increase the triangulation accuracy, we introduce a depth-refinement network (DRN) that optimizes the initial depth map based on the image's contextual cues. In particular, the DRN contains an iterative refinement module (IRM) that improves the depth accuracy over iterations by refining the deep features. Lastly, the DRN also predicts the uncertainty in the refined depths, which is desirable in applications such as measurement selection for scene reconstruction. We show experimentally that our algorithm outperforms state-of-the-art approaches in terms of depth accuracy, and verify that our predicted uncertainty is highly correlated to the actual depth error.

Deep Depth Estimation from Visual-Inertial SLAM

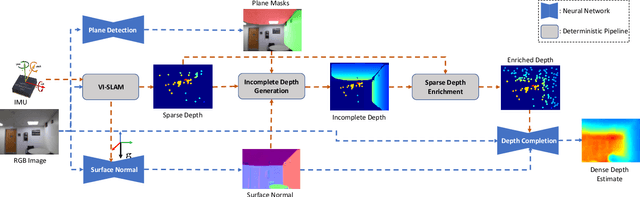
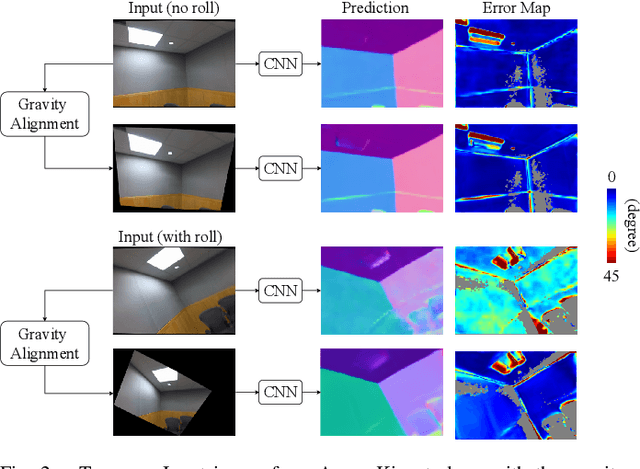
This paper addresses the problem of learning to complete a scene's depth from sparse depth points and images of indoor scenes. Specifically, we study the case in which the sparse depth is computed from a visual-inertial simultaneous localization and mapping (VI-SLAM) system. The resulting point cloud has low density, it is noisy, and has non-uniform spatial distribution, as compared to the input from active depth sensors, e.g., LiDAR or Kinect. Since the VI-SLAM produces point clouds only over textured areas, we compensate for the missing depth of the low-texture surfaces by leveraging their planar structures and their surface normals which is an important intermediate representation. The pre-trained surface normal network, however, suffers from large performance degradation when there is a significant difference in the viewing direction (especially the roll angle) of the test image as compared to the trained ones. To address this limitation, we use the available gravity estimate from the VI-SLAM to warp the input image to the orientation prevailing in the training dataset. This results in a significant performance gain for the surface normal estimate, and thus the dense depth estimates. Finally, we show that our method outperforms other state-of-the-art approaches both on training (ScanNet and NYUv2) and testing (collected with Azure Kinect) datasets.

An Efficient Algebraic Solution to the Perspective-Three-Point Problem

In this work, we present an algebraic solution to the classical perspective-3-point (P3P) problem for determining the position and attitude of a camera from observations of three known reference points. In contrast to previous approaches, we first directly determine the camera's attitude by employing the corresponding geometric constraints to formulate a system of trigonometric equations. This is then efficiently solved, following an algebraic approach, to determine the unknown rotation matrix and subsequently the camera's position. As compared to recent alternatives, our method avoids computing unnecessary (and potentially numerically unstable) intermediate results, and thus achieves higher numerical accuracy and robustness at a lower computational cost. These benefits are validated through extensive Monte-Carlo simulations for both nominal and close-to-singular geometric configurations.