How noise affects memory in linear recurrent networks

The effects of noise on memory in a linear recurrent network are theoretically investigated. Memory is characterized by its ability to store previous inputs in its instantaneous state of network, which receives a correlated or uncorrelated noise. Two major properties are revealed: First, the memory reduced by noise is uniquely determined by the noise's power spectral density (PSD). Second, the memory will not decrease regardless of noise intensity if the PSD is in a certain class of distribution (including power law). The results are verified using the human brain signals, showing good agreement.

Quantum Noise-Induced Reservoir Computing

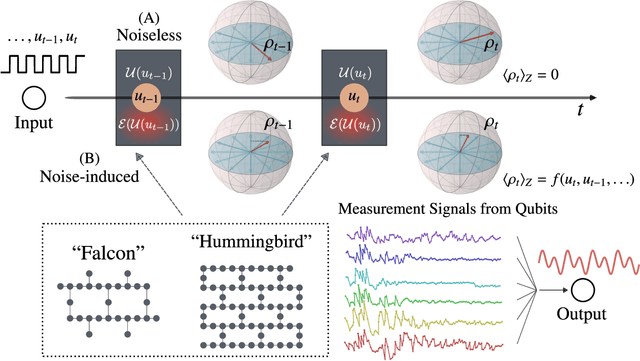
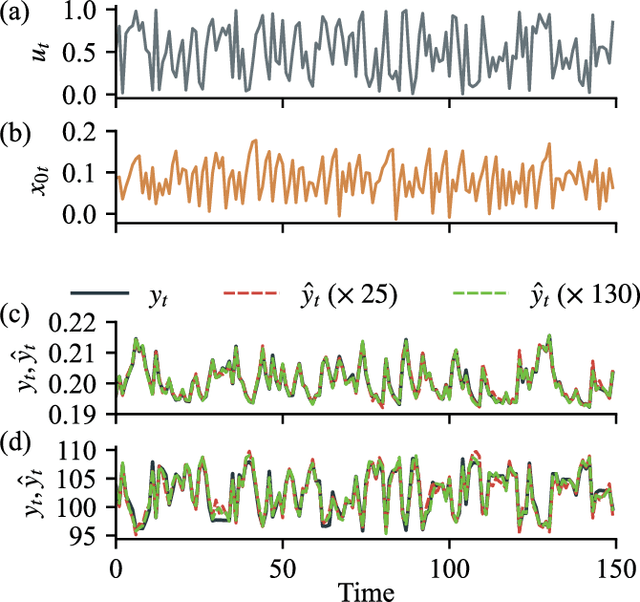
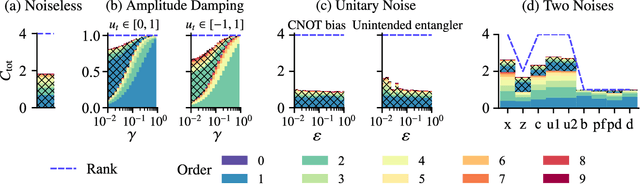
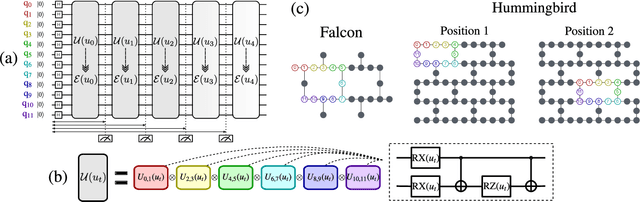
Quantum computing has been moving from a theoretical phase to practical one, presenting daunting challenges in implementing physical qubits, which are subjected to noises from the surrounding environment. These quantum noises are ubiquitous in quantum devices and generate adverse effects in the quantum computational model, leading to extensive research on their correction and mitigation techniques. But do these quantum noises always provide disadvantages? We tackle this issue by proposing a framework called quantum noise-induced reservoir computing and show that some abstract quantum noise models can induce useful information processing capabilities for temporal input data. We demonstrate this ability in several typical benchmarks and investigate the information processing capacity to clarify the framework's processing mechanism and memory profile. We verified our perspective by implementing the framework in a number of IBM quantum processors and obtained similar characteristic memory profiles with model analyses. As a surprising result, information processing capacity increased with quantum devices' higher noise levels and error rates. Our study opens up a novel path for diverting useful information from quantum computer noises into a more sophisticated information processor.

Dynamical Anatomy of NARMA10 Benchmark Task

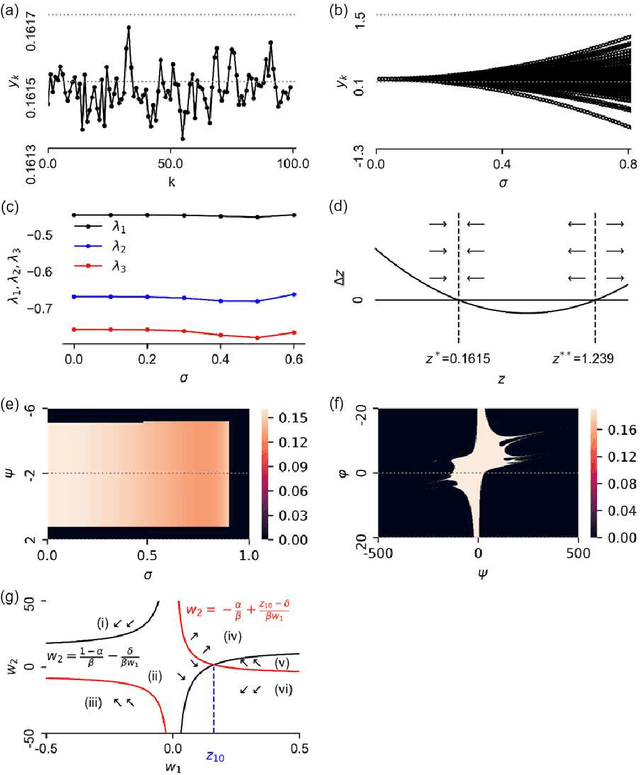
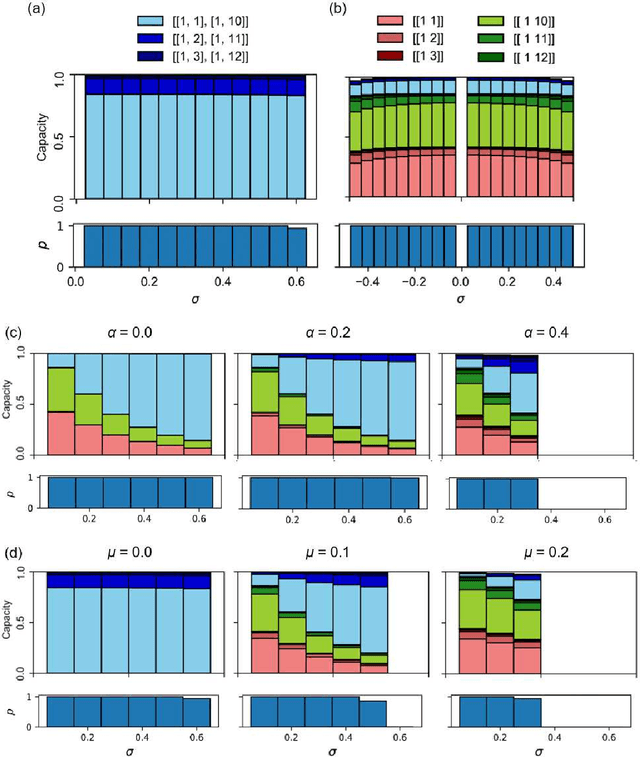
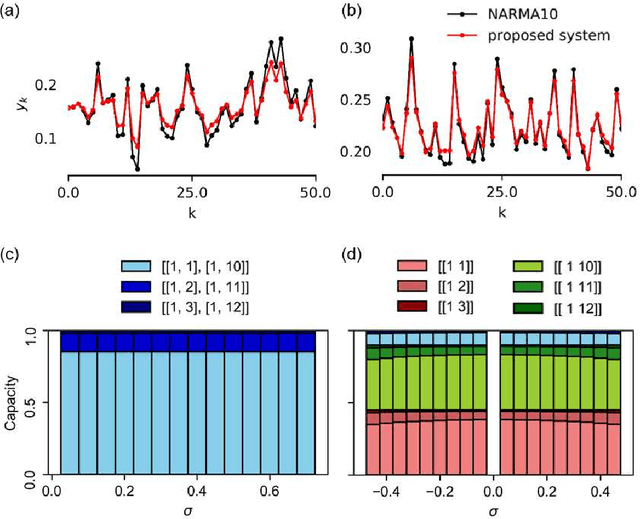
The emulation task of a nonlinear autoregressive moving average model, i.e., the NARMA10 task, has been widely used as a benchmark task for recurrent neural networks, especially in reservoir computing. However, the type and quantity of computational capabilities required to emulate the NARMA10 model remain unclear, and, to date, the NARMA10 task has been utilized blindly. Therefore, in this study, we have investigated the properties of the NARMA10 model from a dynamical system perspective. We revealed its bifurcation structure and basin of attraction, as well as the system's Lyapunov spectra. Furthermore, we have analyzed the computational capabilities required to emulate the NARMA10 model by decomposing it into multiple combinations of orthogonal nonlinear polynomials using Legendre polynomials, and we directly evaluated its information processing capacity together with its dependences on some system parameters. The result demonstrates that the NARMA10 model contains an unstable region in the phase space that makes the system diverge according to the selection of the input range and initial conditions. Furthermore, the information processing capacity of the model varies according to the input range. These properties prevent safe application of this model and fair comparisons among experiments, which are unfavorable for a benchmark task. As a result, we propose a benchmark model that can clearly evaluate equivalent computational capacity using NARMA10. Compared to the original NARMA10 model, the proposed model is highly stable and robust against the input range settings.