Cellular, Cell-less, and Everything in Between: A Unified Framework for Utility Region Analysis in Wireless Networks

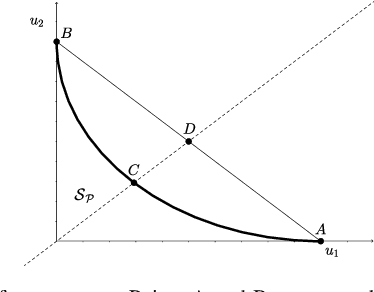
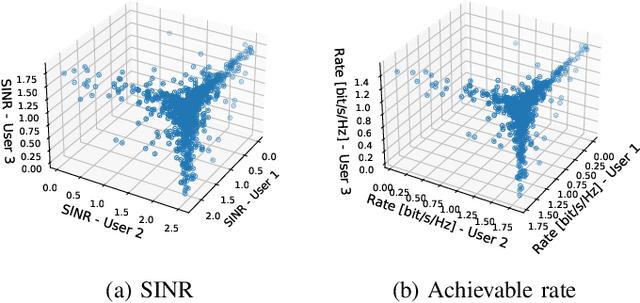
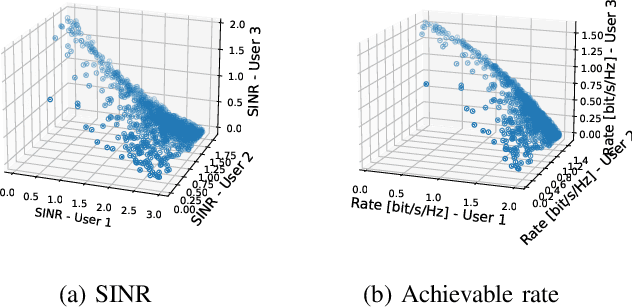
We introduce a unified framework for analyzing utility regions of wireless networks, with a focus on the signal-to-interference-noise-ratio (SINR) and achievable rate regions. The framework provides valuable insights into interference patterns of modern network architectures, such as cell-less and extremely large MIMO networks, and it generalizes existing characterizations of the weak Pareto boundary. A central contribution is the derivation of sufficient conditions that guarantee convexity of the utility regions. Convexity is an important property because it ensures that time sharing (or user grouping) cannot simultaneously increase the utility of all users when the network operates on the weak Pareto boundary. These sufficient conditions also have two key implications. First, they identify a family of (weighted) sum-rate maximization problems that are inherently convex without any variable transformations, thus paving the way for the development of efficient, provably optimal solvers for this family. Second, they provide a rigorous justification for formulating sum-rate maximization problems directly in terms of achievable rates, rather than SINR levels. Our theoretical insights also motivate an alternative to the concept of favorable propagation in the massive MIMO literature -- one that explicitly accounts for self-interference and the beamforming strategy.

Positive concave deep equilibrium models

Deep equilibrium (DEQ) models are widely recognized as a memory efficient alternative to standard neural networks, achieving state-of-the-art performance in language modeling and computer vision tasks. These models solve a fixed point equation instead of explicitly computing the output, which sets them apart from standard neural networks. However, existing DEQ models often lack formal guarantees of the existence and uniqueness of the fixed point, and the convergence of the numerical scheme used for computing the fixed point is not formally established. As a result, DEQ models are potentially unstable in practice. To address these drawbacks, we introduce a novel class of DEQ models called positive concave deep equilibrium (pcDEQ) models. Our approach, which is based on nonlinear Perron-Frobenius theory, enforces nonnegative weights and activation functions that are concave on the positive orthant. By imposing these constraints, we can easily ensure the existence and uniqueness of the fixed point without relying on additional complex assumptions commonly found in the DEQ literature, such as those based on monotone operator theory in convex analysis. Furthermore, the fixed point can be computed with the standard fixed point algorithm, and we provide theoretical guarantees of geometric convergence, which, in particular, simplifies the training process. Experiments demonstrate the competitiveness of our pcDEQ models against other implicit models.

Inverse Solvability and Security with Applications to Federated Learning

We introduce the concepts of inverse solvability and security for a generic linear forward model and demonstrate how they can be applied to models used in federated learning. We provide examples of such models which differ in the resulting inverse solvability and security as defined in this paper. We also show how the large number of users participating in a given iteration of federated learning can be leveraged to increase both solvability and security. Finally, we discuss possible extensions of the presented concepts including the nonlinear case.

ToFFi -- Toolbox for Frequency-based Fingerprinting of Brain Signals

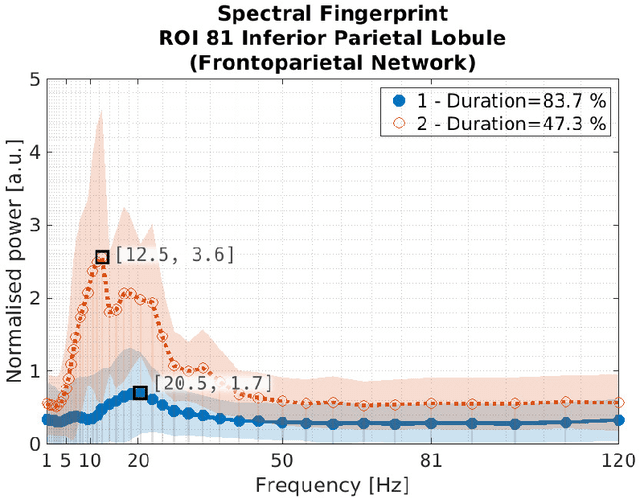
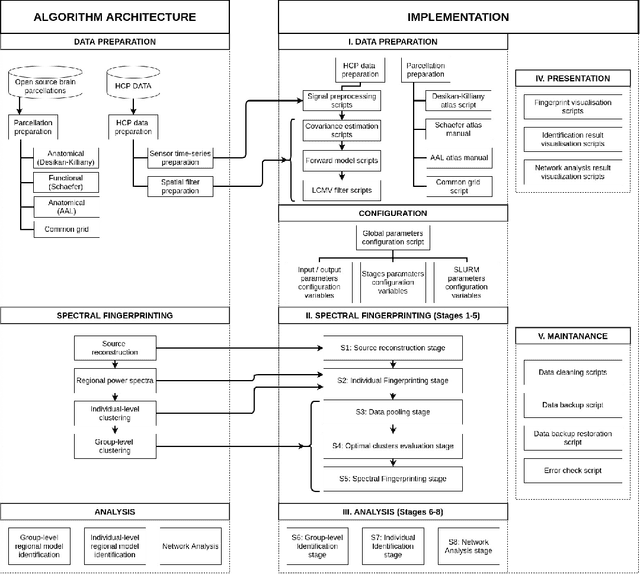
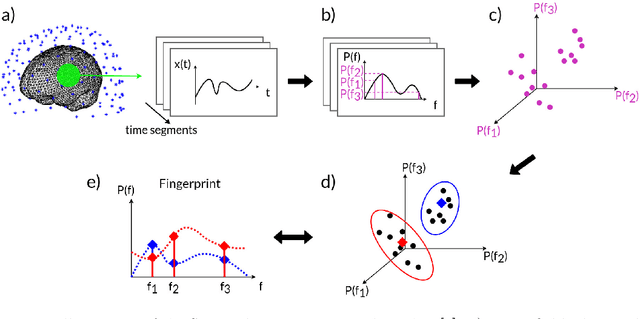
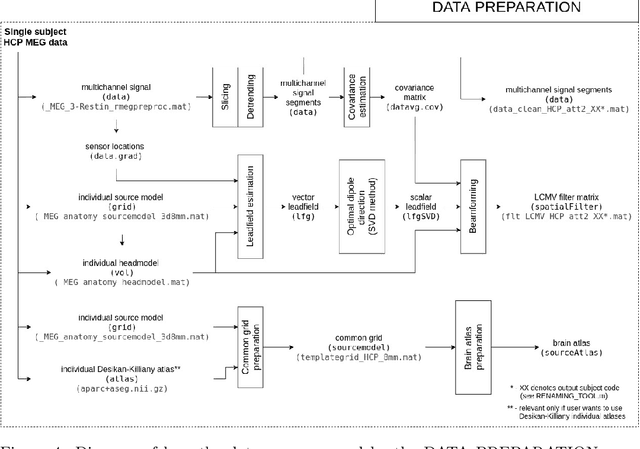
Spectral fingerprints (SFs) are unique power spectra signatures of human brain regions of interest (ROIs, Keitel & Gross, 2016). SFs allow for accurate ROI identification and can serve as biomarkers of differences exhibited by non-neurotypical groups. At present, there are no open-source, versatile tools to calculate spectral fingerprints. We have filled this gap by creating a modular, highly-configurable MATLAB Toolbox for Frequency-based Fingerprinting (ToFFi). It can transform MEG/EEG signals into unique spectral representations using ROIs provided by anatomical (AAL, Desikan-Killiany), functional (Schaefer), or other custom volumetric brain parcellations. Toolbox design supports reproducibility and parallel computations.

Fixed points of monotonic and scalable neural networks

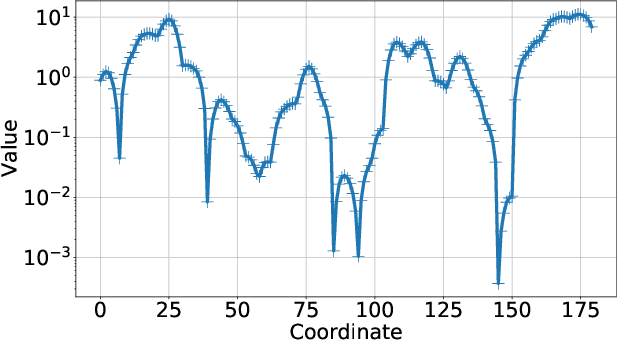
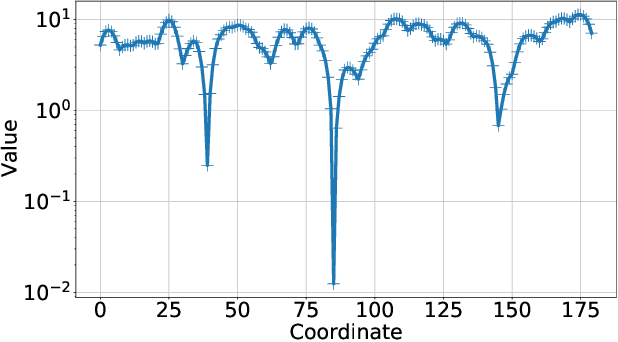
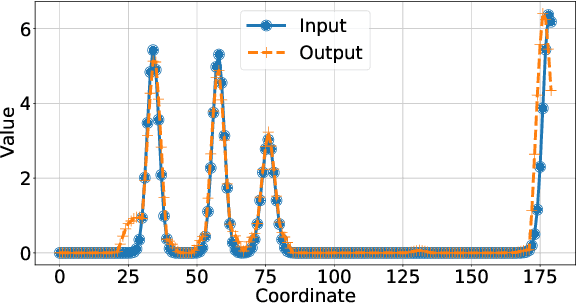
We derive conditions for the existence of fixed points of neural networks, an important research objective to understand their behavior in modern applications involving autoencoders and loop unrolling techniques, among others. In particular, we focus on networks with nonnegative inputs and nonnegative network parameters, as often considered in the literature. We show that such networks can be recognized as monotonic and (weakly) scalable functions within the framework of nonlinear Perron-Frobenius theory. This fact enables us to derive conditions for the existence of a nonempty fixed point set of the neural networks, and these conditions are weaker than those obtained recently using arguments in convex analysis, which are typically based on the assumption of nonexpansivity of the activation functions. Furthermore, we prove that the shape of the fixed point set of monotonic and weakly scalable neural networks is often an interval, which degenerates to a point for the case of scalable networks. The chief results of this paper are verified in numerical simulations, where we consider an autoencoder-type network that first compresses angular power spectra in massive MIMO systems, and, second, reconstruct the input spectra from the compressed signal.

Iterative Neural Networks with Bounded Weights

A recent analysis of a model of iterative neural network in Hilbert spaces established fundamental properties of such networks, such as existence of the fixed points sets, convergence analysis, and Lipschitz continuity. Building on these results, we show that under a single mild condition on the weights of the network, one is guaranteed to obtain a neural network converging to its unique fixed point. We provide a bound on the norm of this fixed point in terms of norms of weights and biases of the network. We also show why this model of a feed-forward neural network is not able to accomodate Hopfield networks under our assumption.