Krzysztof Rykaczewski
Fixed Points of Cone Mapping with the Application to Neural Networks
Jul 20, 2022



Abstract:We derive conditions for the existence of fixed points of cone mappings without assuming scalability of functions. Monotonicity and scalability are often inseparable in the literature in the context of searching for fixed points of interference mappings. In applications, such mappings are approximated by non-negative neural networks. It turns out, however, that the process of training non-negative networks requires imposing an artificial constraint on the weights of the model. However, in the case of specific non-negative data, it cannot be said that if the mapping is non-negative, it has only non-negative weights. Therefore, we considered the problem of the existence of fixed points for general neural networks, assuming the conditions of tangency conditions with respect to specific cones. This does not relax the physical assumptions, because even assuming that the input and output are to be non-negative, the weights can have (small, but) less than zero values. Such properties (often found in papers on the interpretability of weights of neural networks) lead to the weakening of the assumptions about the monotonicity or scalability of the mapping associated with the neural network. To the best of our knowledge, this paper is the first to study this phenomenon.
ToFFi -- Toolbox for Frequency-based Fingerprinting of Brain Signals
Oct 19, 2021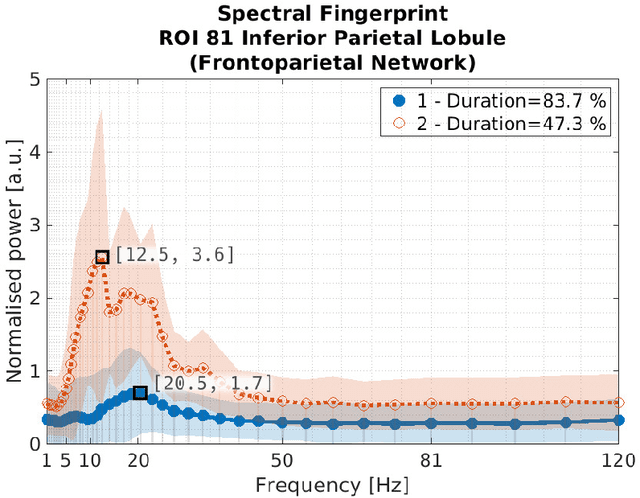
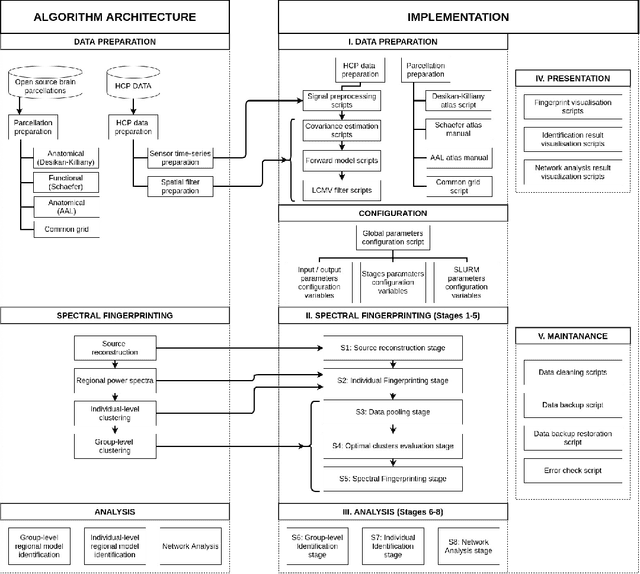
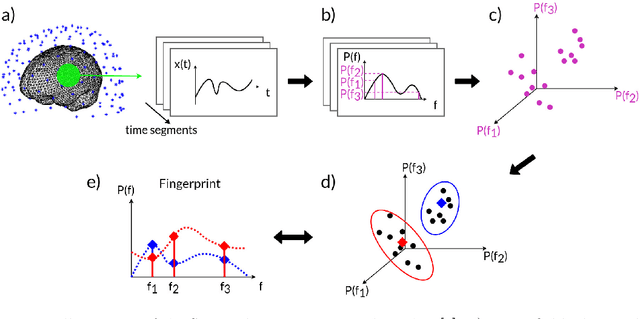
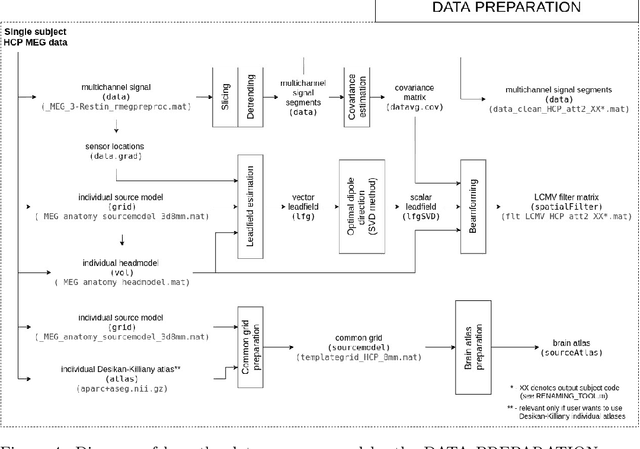
Abstract:Spectral fingerprints (SFs) are unique power spectra signatures of human brain regions of interest (ROIs, Keitel & Gross, 2016). SFs allow for accurate ROI identification and can serve as biomarkers of differences exhibited by non-neurotypical groups. At present, there are no open-source, versatile tools to calculate spectral fingerprints. We have filled this gap by creating a modular, highly-configurable MATLAB Toolbox for Frequency-based Fingerprinting (ToFFi). It can transform MEG/EEG signals into unique spectral representations using ROIs provided by anatomical (AAL, Desikan-Killiany), functional (Schaefer), or other custom volumetric brain parcellations. Toolbox design supports reproducibility and parallel computations.
Deep Learning Based Open Set Acoustic Scene Classification
Aug 17, 2020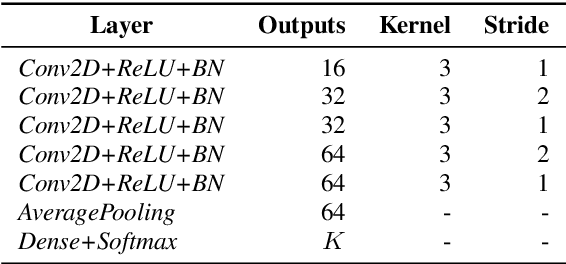
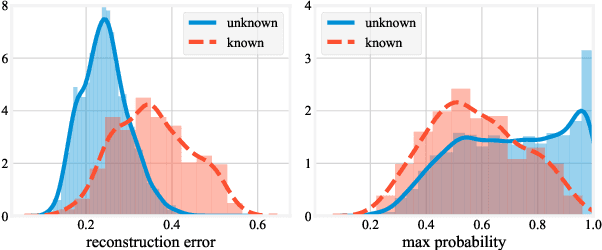
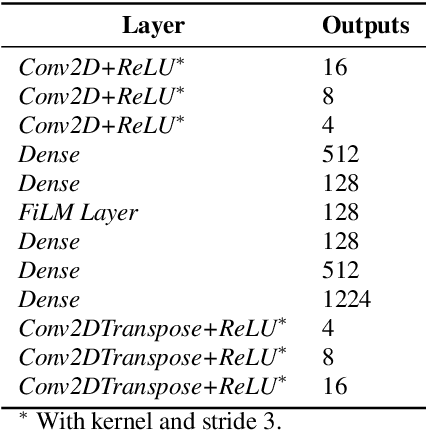
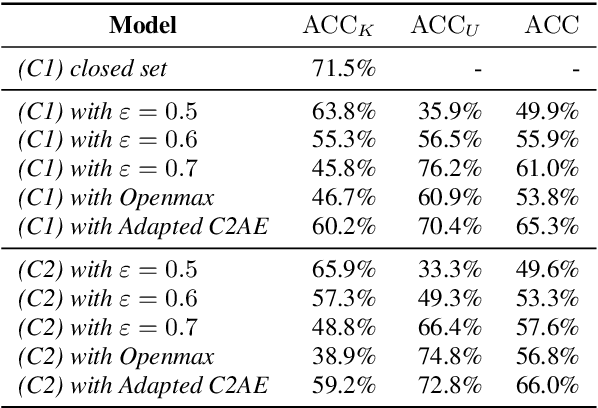
Abstract:In this work, we compare the performance of three selected techniques in open set acoustic scenes classification (ASC). We test thresholding of the softmax output of a deep network classifier, which is the most popular technique nowadays employed in ASC. Further we compare the results with the Openmax classifier which is derived from the computer vision field. As the third model, we use the Adapted Class-Conditioned Autoencoder (Adapted C2AE) which is our variation of another computer vision related technique called C2AE. Adapted C2AE encompasses a more fair comparison of the given experiments and simplifies the original inference procedure, making it more applicable in the real-life scenarios. We also analyse two training scenarios: without additional knowledge of unknown classes and another where a limited subset of examples from the unknown classes is available. We find that the C2AE based method outperforms the thresholding and Openmax, obtaining $85.5\%$ Area Under the Receiver Operating Characteristic curve (AUROC) and $66\%$ of open set accuracy on data used in Detection and Classification of Acoustic Scenes and Events Challenge 2019 Task 1C.
Iterative Neural Networks with Bounded Weights
Aug 19, 2019Abstract:A recent analysis of a model of iterative neural network in Hilbert spaces established fundamental properties of such networks, such as existence of the fixed points sets, convergence analysis, and Lipschitz continuity. Building on these results, we show that under a single mild condition on the weights of the network, one is guaranteed to obtain a neural network converging to its unique fixed point. We provide a bound on the norm of this fixed point in terms of norms of weights and biases of the network. We also show why this model of a feed-forward neural network is not able to accomodate Hopfield networks under our assumption.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge