Reduced storage direct tensor ring decomposition for convolutional neural networks compression

Convolutional neural networks (CNNs) are among the most widely used machine learning models for computer vision tasks, such as image classification. To improve the efficiency of CNNs, many CNNs compressing approaches have been developed. Low-rank methods approximate the original convolutional kernel with a sequence of smaller convolutional kernels, which leads to reduced storage and time complexities. In this study, we propose a novel low-rank CNNs compression method that is based on reduced storage direct tensor ring decomposition (RSDTR). The proposed method offers a higher circular mode permutation flexibility, and it is characterized by large parameter and FLOPS compression rates, while preserving a good classification accuracy of the compressed network. The experiments, performed on the CIFAR-10 and ImageNet datasets, clearly demonstrate the efficiency of RSDTR in comparison to other state-of-the-art CNNs compression approaches.

Non-negative matrix underapproximation as optimal frequency band selector

Time-frequency representation (TFR) is often used for non-stationary signal analysis. The most intuitive and interpretable TFR is the spectrogram. Recently, a concept of non-negative matrix factorization (NMF) has been successfully applied to local damage detection in rolling elements of bearings via spectrogram factorization. NMF applied to the spectrogram allows one to find an informative frequency band, which could be further used as a filter characteristic. However, the obtained filter characteristics mostly detect the informative frequency band, which also encompasses a lot of noise. In the case where noise is more problematic, as is the case for acoustic signals from industrial machines, the NMF hardly detects the damage. To solve this problem and obtain more selective filters, which are more robust to noise, we propose the non-negative matrix under-approximation (NMU) as an informative frequency band selector. Due to the more sparse parts-based representation of the NMU compared to NMF, NMU provides more selective filter characteristics, which neglect the non-informative frequency bands related to the noise. In practice, it means that NMU gives a better signal-to-noise ratio for the filtered signal. The efficiency of the proposed approach has been validated on the vibration signal from the test rig and the acoustic signal from an idler.

Bearing damage detection with orthogonal and non-negative low-rank feature extraction

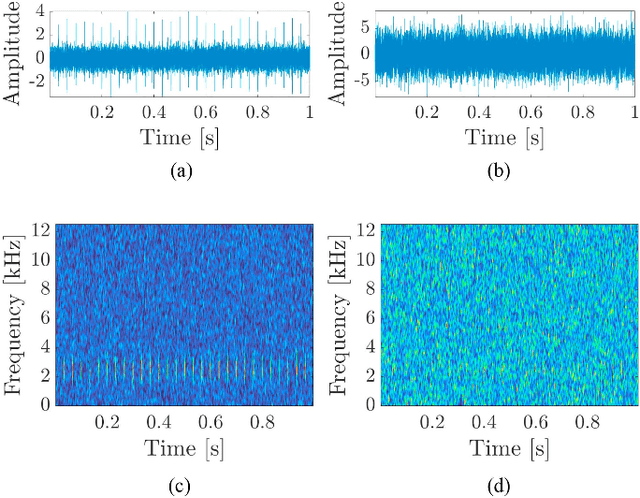
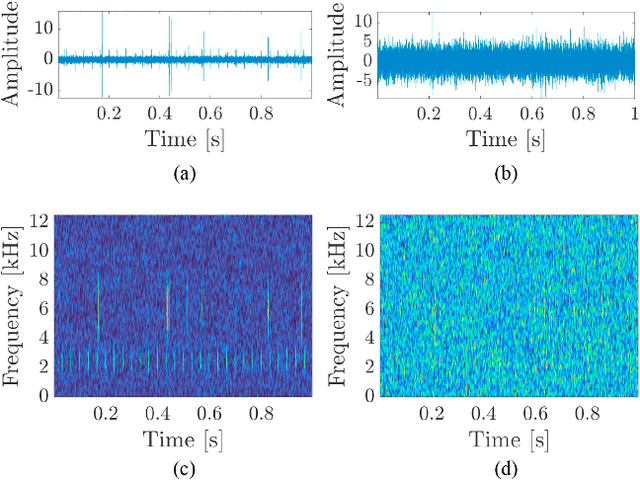
Local damage of bearings can be detected as a weak cyclic and impulsive component in a highly noisy measured signal. A key problem is how to extract the signal of interest (SOI) from the raw signal, i.e., how to identify and design an optimal filter. To tackle this problem, we propose to use stochastic sampled orthogonal non-negative matrix factorization for extracting frequency-based features from a spectrogram of the measured signal. The proposed algorithm finds a selective filter that is tailored to the frequency band of the SOI. We show that our approach outperforms the other state-of-the-art selectors that were previously used in condition monitoring. The efficiency of the proposed method is illustrated using both a simulation study and the following real signals: (a) vibration signal from a test rig in the laboratory and (b) acoustic signal from a belt conveyor.

Non-negative tensor factorization for vibration-based local damage detection

In this study, a novel non-negative tensor factorization (NTF)-based method for vibration-based local damage detection in rolling element bearings is proposed. As the diagnostic signal registered from a faulty machine is non-stationary, the time-frequency method is frequently used as a primary decomposition technique. It is proposed here to extract multi-linear NTF-based components from a 3D array of time-frequency representations of an observed signal partitioned into blocks. As a result, frequency and temporal informative components can be efficiently separated from non-informative ones. The experiments performed on synthetic and real signals demonstrate the high efficiency of the proposed method with respect to the already known non-negative matrix factorization approach.

Positive concave deep equilibrium models

Deep equilibrium (DEQ) models are widely recognized as a memory efficient alternative to standard neural networks, achieving state-of-the-art performance in language modeling and computer vision tasks. These models solve a fixed point equation instead of explicitly computing the output, which sets them apart from standard neural networks. However, existing DEQ models often lack formal guarantees of the existence and uniqueness of the fixed point, and the convergence of the numerical scheme used for computing the fixed point is not formally established. As a result, DEQ models are potentially unstable in practice. To address these drawbacks, we introduce a novel class of DEQ models called positive concave deep equilibrium (pcDEQ) models. Our approach, which is based on nonlinear Perron-Frobenius theory, enforces nonnegative weights and activation functions that are concave on the positive orthant. By imposing these constraints, we can easily ensure the existence and uniqueness of the fixed point without relying on additional complex assumptions commonly found in the DEQ literature, such as those based on monotone operator theory in convex analysis. Furthermore, the fixed point can be computed with the standard fixed point algorithm, and we provide theoretical guarantees of geometric convergence, which, in particular, simplifies the training process. Experiments demonstrate the competitiveness of our pcDEQ models against other implicit models.