A majorized PAM method with subspace correction for low-rank composite factorization model

This paper concerns a class of low-rank composite factorization models arising from matrix completion. For this nonconvex and nonsmooth optimization problem, we propose a proximal alternating minimization algorithm (PAMA) with subspace correction, in which a subspace correction step is imposed on every proximal subproblem so as to guarantee that the corrected proximal subproblem has a closed-form solution. For this subspace correction PAMA, we prove the subsequence convergence of the iterate sequence, and establish the convergence of the whole iterate sequence and the column subspace sequences of factor pairs under the KL property of objective function and a restrictive condition that holds automatically for the column $\ell_{2,0}$-norm function. Numerical comparison with the proximal alternating linearized minimization method on one-bit matrix completion problems indicates that PAMA has an advantage in seeking lower relative error within less time.

An inexact linearized proximal algorithm for a class of DC composite optimization problems and applications

This paper is concerned with a class of DC composite optimization problems which, as an extension of the convex composite optimization problem and the DC program with nonsmooth components, often arises from robust factorization models of low-rank matrix recovery. For this class of nonconvex and nonsmooth problems, we propose an inexact linearized proximal algorithm (iLPA) which in each step computes an inexact minimizer of a strongly convex majorization constructed by the partial linearization of their objective functions. The generated iterate sequence is shown to be convergent under the Kurdyka-{\L}ojasiewicz (KL) property of a potential function, and the convergence admits a local R-linear rate if the potential function has the KL property of exponent $1/2$ at the limit point. For the latter assumption, we provide a verifiable condition by leveraging the composite structure, and clarify its relation with the regularity used for the convex composite optimization. Finally, the proposed iLPA is applied to a robust factorization model for matrix completions with outliers, DC programs with nonsmooth components, and $\ell_1$-norm exact penalty of DC constrained programs, and numerical comparison with the existing algorithms confirms the superiority of our iLPA in computing time and quality of solutions.

Column $\ell_{2,0}$-norm regularized factorization model of low-rank matrix recovery and its computation

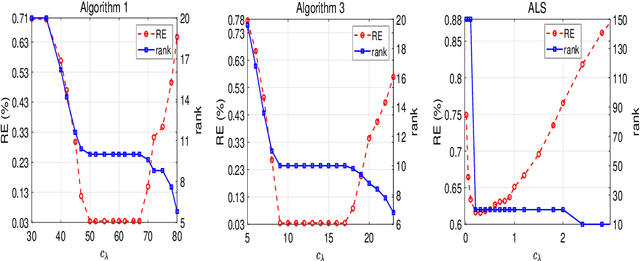
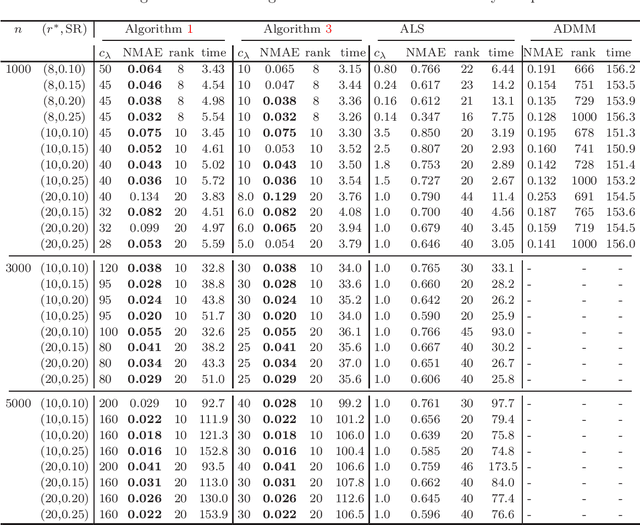
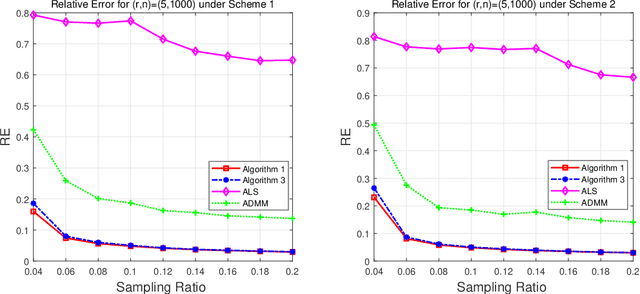
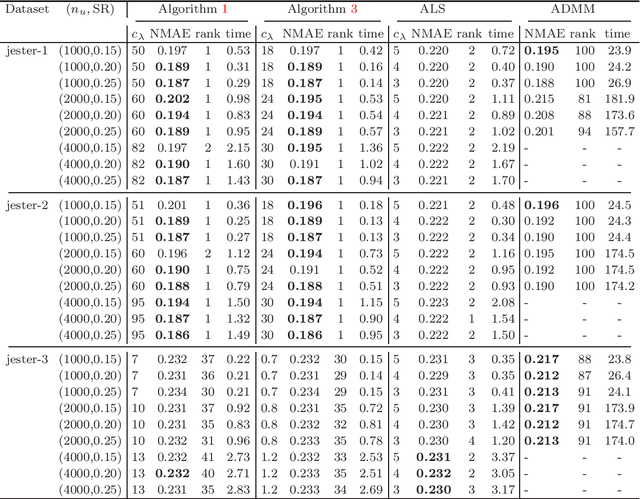
This paper is concerned with the column $\ell_{2,0}$-regularized factorization model of low-rank matrix recovery problems and its computation. The column $\ell_{2,0}$-norm of factor matrices is introduced to promote column sparsity of factors and lower rank solutions. For this nonconvex nonsmooth and non-Lipschitz problem, we develop an alternating majorization-minimization (AMM) method with extrapolation, and a hybrid AMM in which a majorized alternating proximal method is first proposed to seek an initial factor pair with less nonzero columns and then the AMM with extrapolation is applied to the minimization of smooth nonconvex loss. We provide the global convergence analysis for the proposed AMM methods and apply them to the matrix completion problem with non-uniform sampling schemes. Numerical experiments are conducted with synthetic and real data examples, and comparison results with the nuclear-norm regularized factorization model and the max-norm regularized convex model demonstrate that the column $\ell_{2,0}$-regularized factorization model has an advantage in offering solutions of lower error and rank within less time.

Error bound of local minima and KL property of exponent 1/2 for squared F-norm regularized factorization

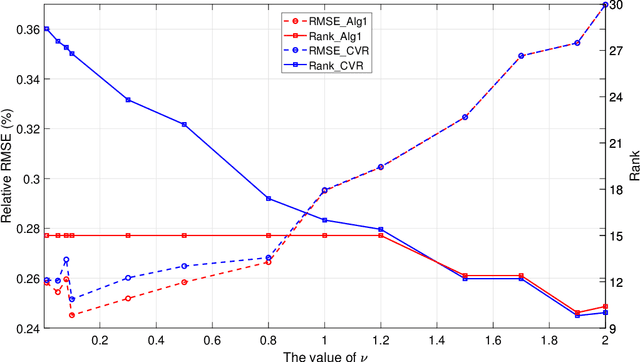
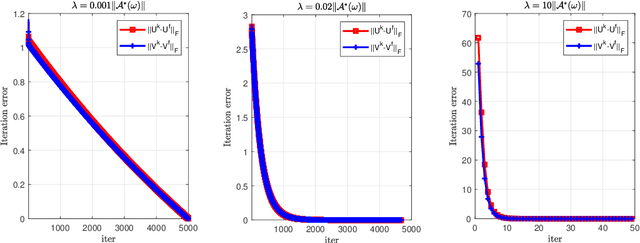
This paper is concerned with the squared F(robenius)-norm regularized factorization form for noisy low-rank matrix recovery problems. Under a suitable assumption on the restricted condition number of the Hessian matrix of the loss function, we establish an error bound to the true matrix for those local minima whose ranks are not more than the rank of the true matrix. Then, for the least squares loss function, we achieve the KL property of exponent 1/2 for the F-norm regularized factorization function over its global minimum set under a restricted strong convexity assumption. These theoretical findings are also confirmed by applying an accelerated alternating minimization method to the F-norm regularized factorization problem.

KL property of exponent $1/2$ of $\ell_{2,0}$-norm and DC regularized factorizations for low-rank matrix recovery

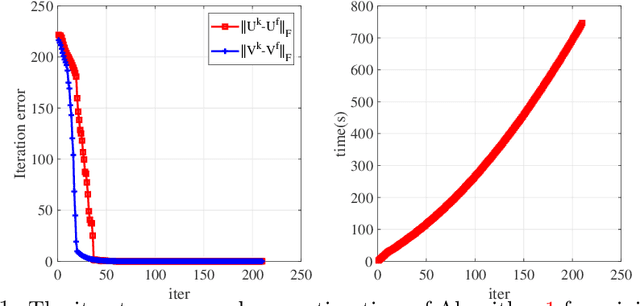
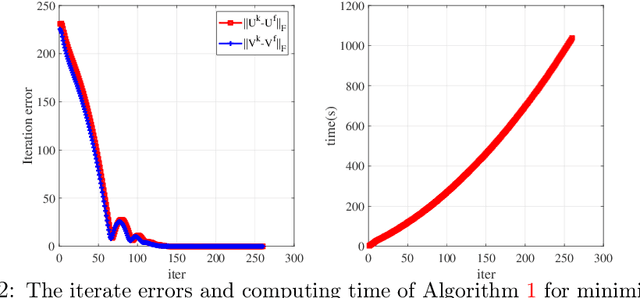
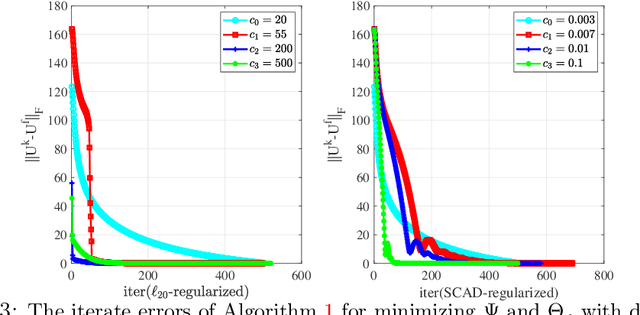
This paper is concerned with the factorization form of the rank regularized loss minimization problem. To cater for the scenario in which only a coarse estimation is available for the rank of the true matrix, an $\ell_{2,0}$-norm regularized term is added to the factored loss function to reduce the rank adaptively; and account for the ambiguities in the factorization, a balanced term is then introduced. For the least squares loss, under a restricted condition number assumption on the sampling operator, we establish the KL property of exponent $1/2$ of the nonsmooth factored composite function and its equivalent DC reformulations in the set of their global minimizers. We also confirm the theoretical findings by applying a proximal linearized alternating minimization method to the regularized factorizations.