Error bound of local minima and KL property of exponent 1/2 for squared F-norm regularized factorization

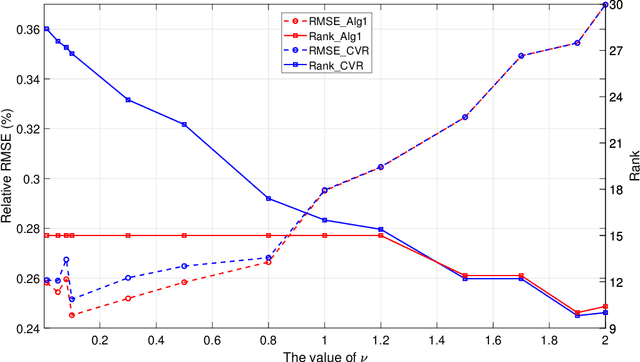
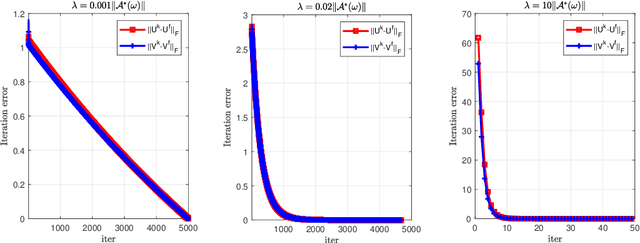
This paper is concerned with the squared F(robenius)-norm regularized factorization form for noisy low-rank matrix recovery problems. Under a suitable assumption on the restricted condition number of the Hessian matrix of the loss function, we establish an error bound to the true matrix for those local minima whose ranks are not more than the rank of the true matrix. Then, for the least squares loss function, we achieve the KL property of exponent 1/2 for the F-norm regularized factorization function over its global minimum set under a restricted strong convexity assumption. These theoretical findings are also confirmed by applying an accelerated alternating minimization method to the F-norm regularized factorization problem.