KL property of exponent $1/2$ of $\ell_{2,0}$-norm and DC regularized factorizations for low-rank matrix recovery
Paper and Code
Aug 24, 2019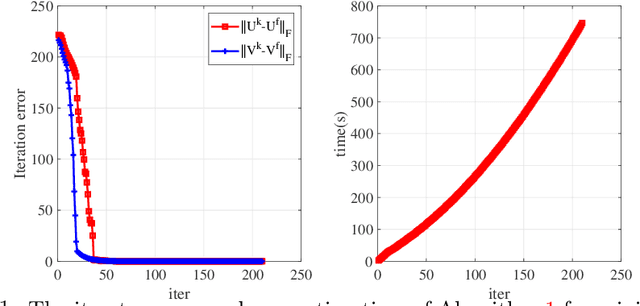
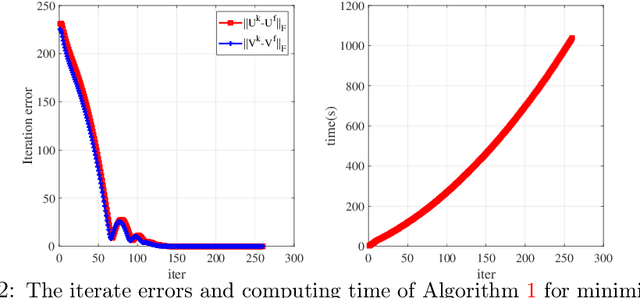
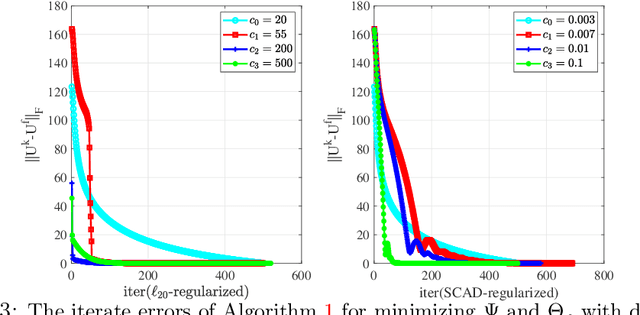
This paper is concerned with the factorization form of the rank regularized loss minimization problem. To cater for the scenario in which only a coarse estimation is available for the rank of the true matrix, an $\ell_{2,0}$-norm regularized term is added to the factored loss function to reduce the rank adaptively; and account for the ambiguities in the factorization, a balanced term is then introduced. For the least squares loss, under a restricted condition number assumption on the sampling operator, we establish the KL property of exponent $1/2$ of the nonsmooth factored composite function and its equivalent DC reformulations in the set of their global minimizers. We also confirm the theoretical findings by applying a proximal linearized alternating minimization method to the regularized factorizations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge