Channel Tracking for RIS-aided mmWave Communications Under High Mobility Scenarios

The emerging reconfigurable intelligent surface (RIS) technology is promising for applications in the millimeter wave (mmWave) communication systems to effectively compensate for propagation loss or tackle the blockage issue. Considering the high mobility of users in realistic scenarios, it is essential to adjust the phase shifts in real time to align the beam towards the mobile users, which requires to frequently estimate the channel state information. Hence, it is imperative to design efficient channel tracking schemes to avoid the complex channel estimation procedure. In this paper, we develop a novel channel tracking scheme with two advantages over conventional schemes. First, our tracking scheme is based on the cascaded angles at the RIS instead of the accurate angle values, which is more practical. Second, it can be employed under a more general setting where the noise can be non-Gaussian. Simulation results show the high tracking accuracy of our proposed scheme, and validate the superiority to the existing EKF-based tracking scheme.

DISK: Domain-constrained Instance Sketch for Math Word Problem Generation

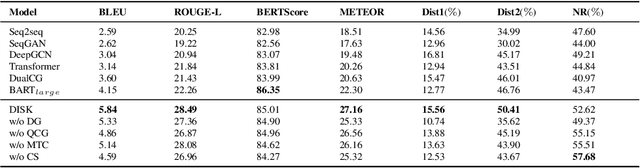
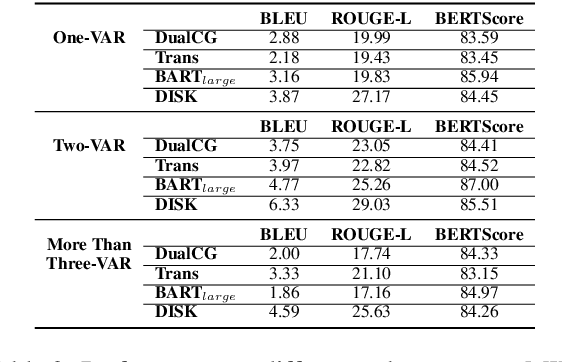
A math word problem (MWP) is a coherent narrative which reflects the underlying logic of math equations. Successful MWP generation can automate the writing of mathematics questions. Previous methods mainly generate MWP text based on inflexible pre-defined templates. In this paper, we propose a neural model for generating MWP text from math equations. Firstly, we incorporate a matching model conditioned on the domain knowledge to retrieve a MWP instance which is most consistent with the ground-truth, where the domain is a latent variable extracted with a domain summarizer. Secondly, by constructing a Quantity Cell Graph (QCG) from the retrieved MWP instance and reasoning over it, we improve the model's comprehension of real-world scenarios and derive a domain-constrained instance sketch to guide the generation. Besides, the QCG also interacts with the equation encoder to enhance the alignment between math tokens (e.g., quantities and variables) and MWP text. Experiments and empirical analysis on educational MWP set show that our model achieves impressive performance in both automatic evaluation metrics and human evaluation metrics.

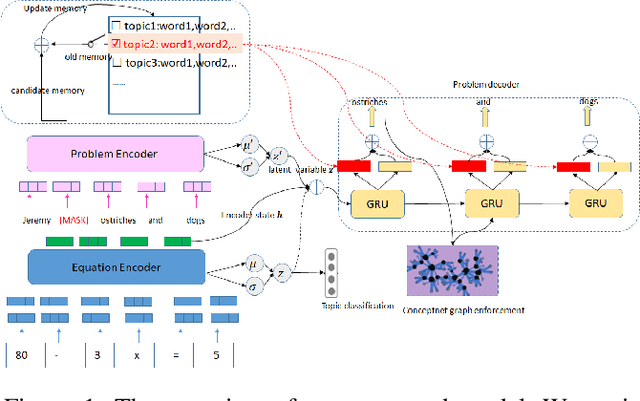
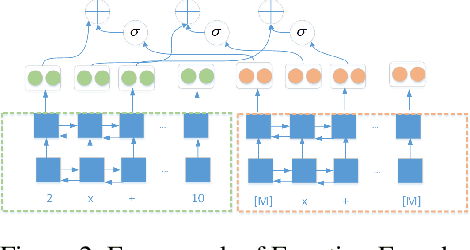
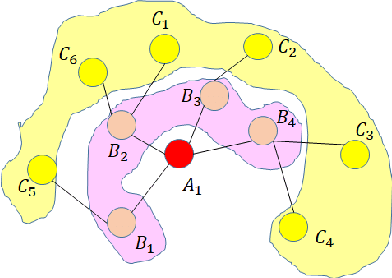
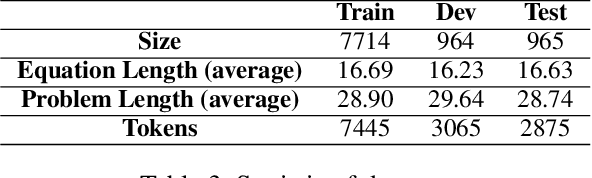
Generating Math Word Problems from Equations with Topic Controlling and Commonsense Enforcement

Recent years have seen significant advancement in text generation tasks with the help of neural language models. However, there exists a challenging task: generating math problem text based on mathematical equations, which has made little progress so far. In this paper, we present a novel equation-to-problem text generation model. In our model, 1) we propose a flexible scheme to effectively encode math equations, we then enhance the equation encoder by a Varitional Autoen-coder (VAE) 2) given a math equation, we perform topic selection, followed by which a dynamic topic memory mechanism is introduced to restrict the topic distribution of the generator 3) to avoid commonsense violation in traditional generation model, we pretrain word embedding with background knowledge graph (KG), and we link decoded words to related words in KG, targeted at injecting background knowledge into our model. We evaluate our model through both automatic metrices and human evaluation, experiments demonstrate our model outperforms baseline and previous models in both accuracy and richness of generated problem text.