Tianduo Wang
From Tens of Hours to Tens of Thousands: Scaling Back-Translation for Speech Recognition
May 22, 2025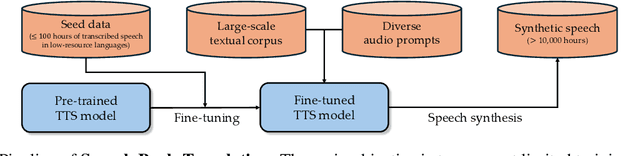
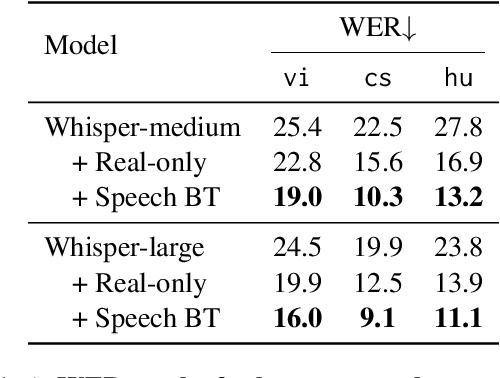
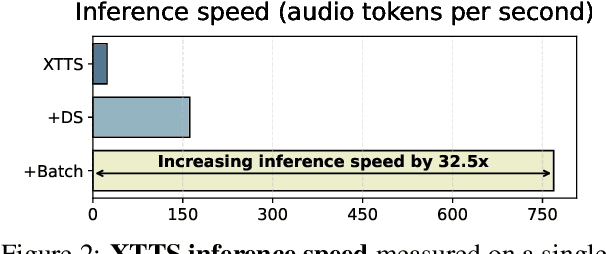

Abstract:Recent advances in Automatic Speech Recognition (ASR) have been largely fueled by massive speech corpora. However, extending coverage to diverse languages with limited resources remains a formidable challenge. This paper introduces Speech Back-Translation, a scalable pipeline that improves multilingual ASR models by converting large-scale text corpora into synthetic speech via off-the-shelf text-to-speech (TTS) models. We demonstrate that just tens of hours of real transcribed speech can effectively train TTS models to generate synthetic speech at hundreds of times the original volume while maintaining high quality. To evaluate synthetic speech quality, we develop an intelligibility-based assessment framework and establish clear thresholds for when synthetic data benefits ASR training. Using Speech Back-Translation, we generate more than 500,000 hours of synthetic speech in ten languages and continue pre-training Whisper-large-v3, achieving average transcription error reductions of over 30\%. These results highlight the scalability and effectiveness of Speech Back-Translation for enhancing multilingual ASR systems.
Self-Training with Direct Preference Optimization Improves Chain-of-Thought Reasoning
Jul 25, 2024



Abstract:Effective training of language models (LMs) for mathematical reasoning tasks demands high-quality supervised fine-tuning data. Besides obtaining annotations from human experts, a common alternative is sampling from larger and more powerful LMs. However, this knowledge distillation approach can be costly and unstable, particularly when relying on closed-source, proprietary LMs like GPT-4, whose behaviors are often unpredictable. In this work, we demonstrate that the reasoning abilities of small-scale LMs can be enhanced through self-training, a process where models learn from their own outputs. We also show that the conventional self-training can be further augmented by a preference learning algorithm called Direct Preference Optimization (DPO). By integrating DPO into self-training, we leverage preference data to guide LMs towards more accurate and diverse chain-of-thought reasoning. We evaluate our method across various mathematical reasoning tasks using different base models. Our experiments show that this approach not only improves LMs' reasoning performance but also offers a more cost-effective and scalable solution compared to relying on large proprietary LMs.
TinyLlama: An Open-Source Small Language Model
Jan 04, 2024



Abstract:We present TinyLlama, a compact 1.1B language model pretrained on around 1 trillion tokens for approximately 3 epochs. Building on the architecture and tokenizer of Llama 2, TinyLlama leverages various advances contributed by the open-source community (e.g., FlashAttention), achieving better computational efficiency. Despite its relatively small size, TinyLlama demonstrates remarkable performance in a series of downstream tasks. It significantly outperforms existing open-source language models with comparable sizes. Our model checkpoints and code are publicly available on GitHub at https://github.com/jzhang38/TinyLlama.
Learning Multi-Step Reasoning by Solving Arithmetic Tasks
Jun 07, 2023
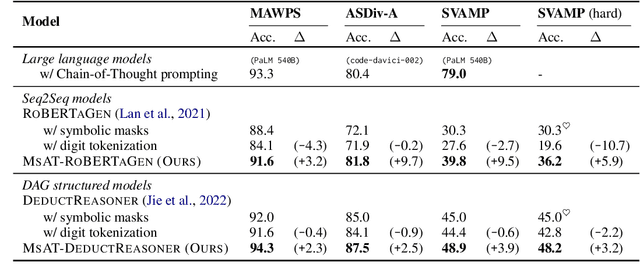
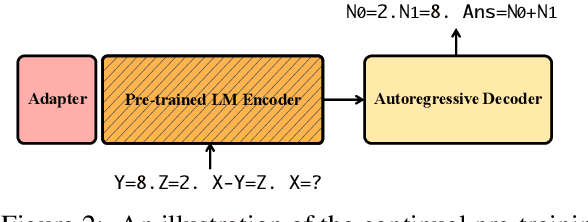
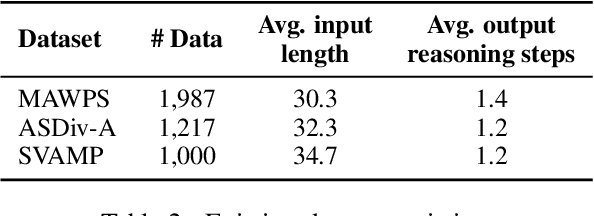
Abstract:Mathematical reasoning is regarded as a necessary ability for Language Models (LMs). Recent works demonstrate large LMs' impressive performance in solving math problems. The success is attributed to their Chain-of-Thought (CoT) reasoning abilities, i.e., the ability to decompose complex questions into step-by-step reasoning chains, but such ability seems only to emerge from models with abundant parameters. This work investigates how to incorporate relatively small LMs with the capabilities of multi-step reasoning. We propose to inject such abilities by continually pre-training LMs on a synthetic dataset MsAT which is composed of Multi-step Arithmetic Tasks. Our experiments on four math word problem datasets show the effectiveness of the proposed method in enhancing LMs' math reasoning abilities.
Differentiable Data Augmentation for Contrastive Sentence Representation Learning
Oct 29, 2022



Abstract:Fine-tuning a pre-trained language model via the contrastive learning framework with a large amount of unlabeled sentences or labeled sentence pairs is a common way to obtain high-quality sentence representations. Although the contrastive learning framework has shown its superiority on sentence representation learning over previous methods, the potential of such a framework is under-explored so far due to the simple method it used to construct positive pairs. Motivated by this, we propose a method that makes hard positives from the original training examples. A pivotal ingredient of our approach is the use of prefix that is attached to a pre-trained language model, which allows for differentiable data augmentation during contrastive learning. Our method can be summarized in two steps: supervised prefix-tuning followed by joint contrastive fine-tuning with unlabeled or labeled examples. Our experiments confirm the effectiveness of our data augmentation approach. The proposed method yields significant improvements over existing methods under both semi-supervised and supervised settings. Our experiments under a low labeled data setting also show that our method is more label-efficient than the state-of-the-art contrastive learning methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge