A Theoretical Perspective on Subnetwork Contributions to Adversarial Robustness

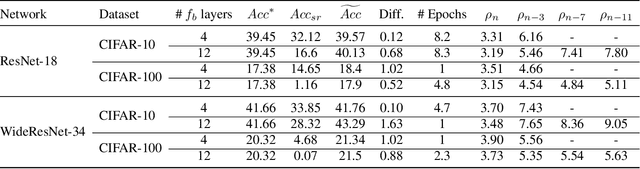
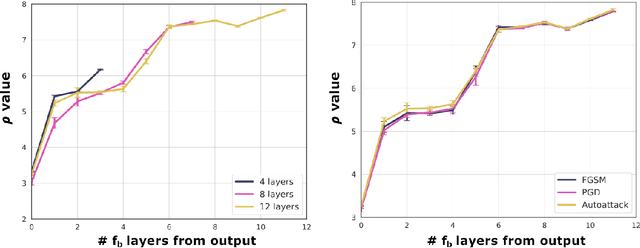
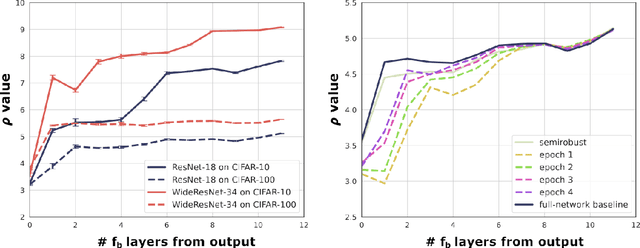
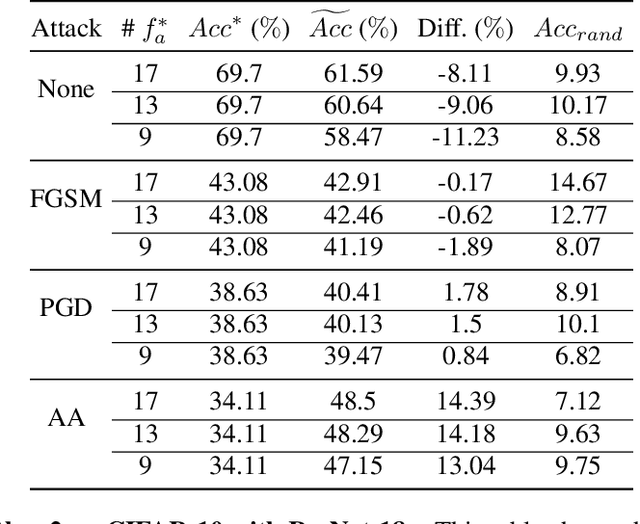
The robustness of deep neural networks (DNNs) against adversarial attacks has been studied extensively in hopes of both better understanding how deep learning models converge and in order to ensure the security of these models in safety-critical applications. Adversarial training is one approach to strengthening DNNs against adversarial attacks, and has been shown to offer a means for doing so at the cost of applying computationally expensive training methods to the entire model. To better understand these attacks and facilitate more efficient adversarial training, in this paper we develop a novel theoretical framework that investigates how the adversarial robustness of a subnetwork contributes to the robustness of the entire network. To do so we first introduce the concept of semirobustness, which is a measure of the adversarial robustness of a subnetwork. Building on this concept, we then provide a theoretical analysis to show that if a subnetwork is semirobust and there is a sufficient dependency between it and each subsequent layer in the network, then the remaining layers are also guaranteed to be robust. We validate these findings empirically across multiple DNN architectures, datasets, and adversarial attacks. Experiments show the ability of a robust subnetwork to promote full-network robustness, and investigate the layer-wise dependencies required for this full-network robustness to be achieved.

Deep Net Triage: Analyzing the Importance of Network Layers via Structural Compression

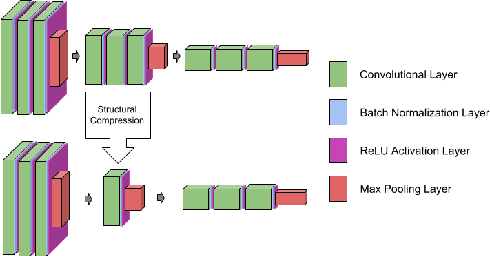
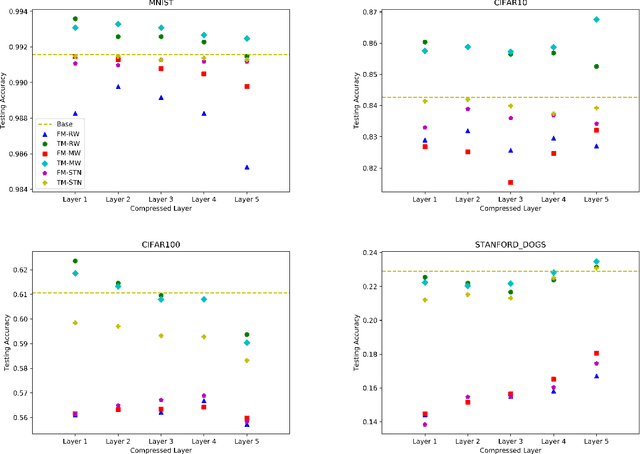
Despite their prevalence, deep networks are poorly understood. This is due, at least in part, to their highly parameterized nature. As such, while certain structures have been found to work better than others, the significance of a model's unique structure, or the importance of a given layer, and how these translate to overall accuracy, remains unclear. In this paper, we analyze these properties of deep neural networks via a process we term deep net triage. Like medical triage---the assessment of the importance of various wounds---we assess the importance of layers in a neural network, or as we call it, their criticality. We do this by applying structural compression, whereby we reduce a block of layers to a single layer. After compressing a set of layers, we apply a combination of initialization and training schemes, and look at network accuracy, convergence, and the layer's learned filters to assess the criticality of the layer. We apply this analysis across four data sets of varying complexity. We find that the accuracy of the model does not depend on which layer was compressed; that accuracy can be recovered or exceeded after compression by fine-tuning across the entire model; and, lastly, that Knowledge Distillation can be used to hasten convergence of a compressed network, but constrains the accuracy attainable to that of the base model.