Deep Net Triage: Analyzing the Importance of Network Layers via Structural Compression
Paper and Code
Mar 22, 2018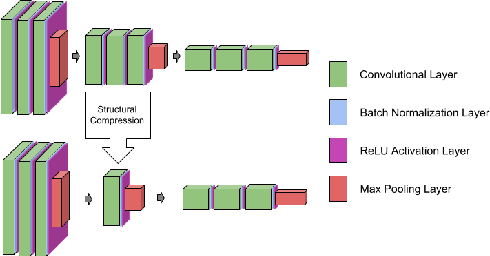


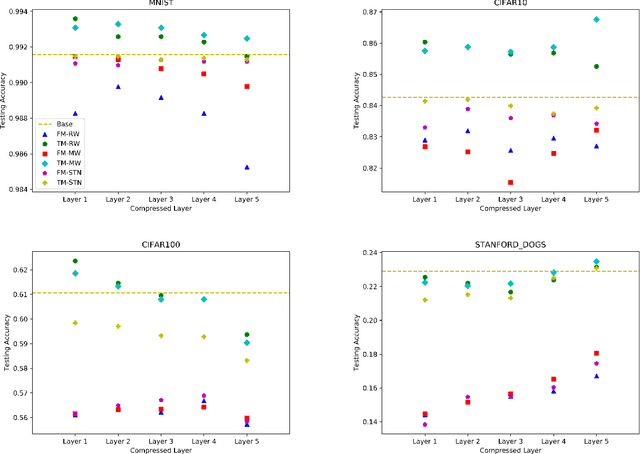
Despite their prevalence, deep networks are poorly understood. This is due, at least in part, to their highly parameterized nature. As such, while certain structures have been found to work better than others, the significance of a model's unique structure, or the importance of a given layer, and how these translate to overall accuracy, remains unclear. In this paper, we analyze these properties of deep neural networks via a process we term deep net triage. Like medical triage---the assessment of the importance of various wounds---we assess the importance of layers in a neural network, or as we call it, their criticality. We do this by applying structural compression, whereby we reduce a block of layers to a single layer. After compressing a set of layers, we apply a combination of initialization and training schemes, and look at network accuracy, convergence, and the layer's learned filters to assess the criticality of the layer. We apply this analysis across four data sets of varying complexity. We find that the accuracy of the model does not depend on which layer was compressed; that accuracy can be recovered or exceeded after compression by fine-tuning across the entire model; and, lastly, that Knowledge Distillation can be used to hasten convergence of a compressed network, but constrains the accuracy attainable to that of the base model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge