A Theoretical Perspective on Subnetwork Contributions to Adversarial Robustness

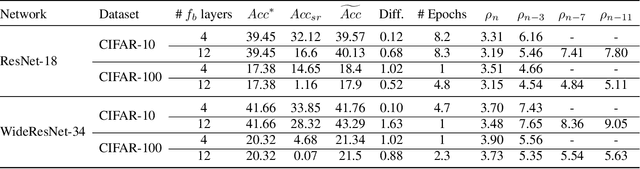
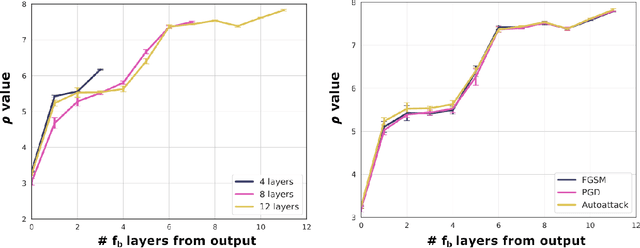
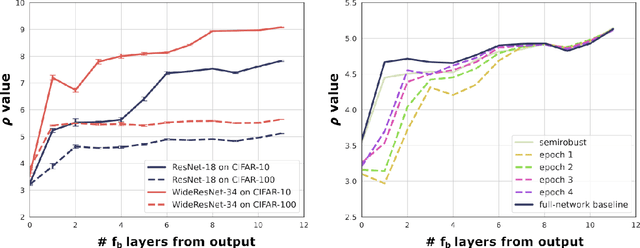
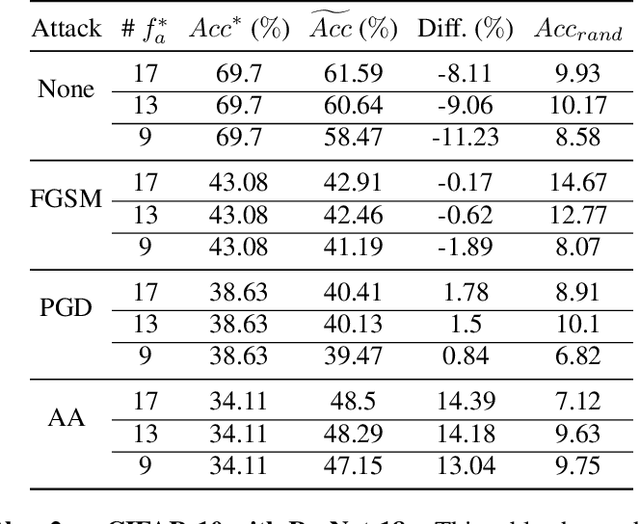
The robustness of deep neural networks (DNNs) against adversarial attacks has been studied extensively in hopes of both better understanding how deep learning models converge and in order to ensure the security of these models in safety-critical applications. Adversarial training is one approach to strengthening DNNs against adversarial attacks, and has been shown to offer a means for doing so at the cost of applying computationally expensive training methods to the entire model. To better understand these attacks and facilitate more efficient adversarial training, in this paper we develop a novel theoretical framework that investigates how the adversarial robustness of a subnetwork contributes to the robustness of the entire network. To do so we first introduce the concept of semirobustness, which is a measure of the adversarial robustness of a subnetwork. Building on this concept, we then provide a theoretical analysis to show that if a subnetwork is semirobust and there is a sufficient dependency between it and each subsequent layer in the network, then the remaining layers are also guaranteed to be robust. We validate these findings empirically across multiple DNN architectures, datasets, and adversarial attacks. Experiments show the ability of a robust subnetwork to promote full-network robustness, and investigate the layer-wise dependencies required for this full-network robustness to be achieved.