Safe Reinforcement Learning for Grid Voltage Control

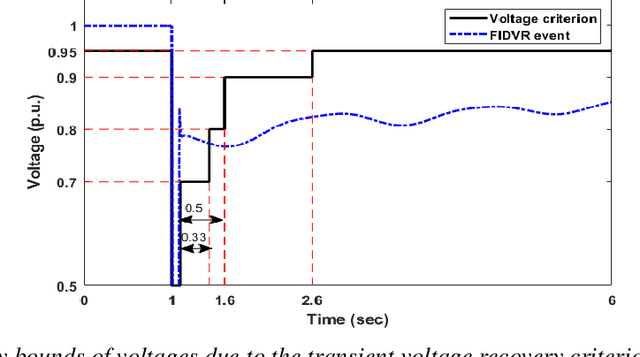
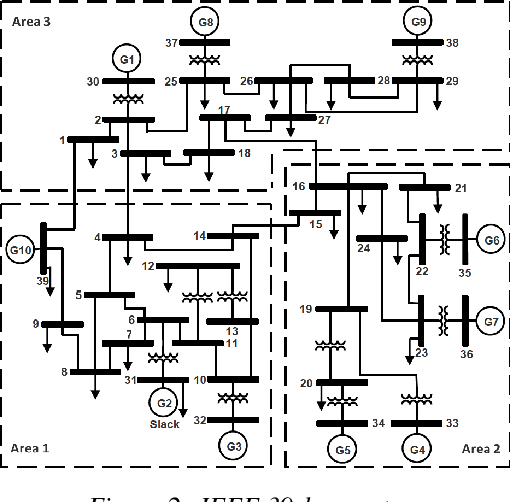
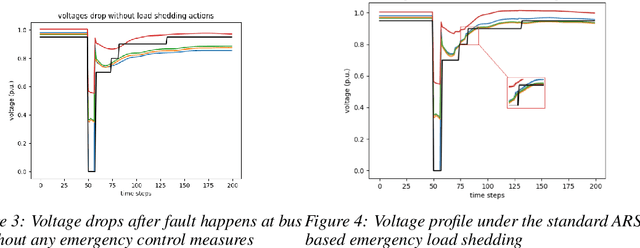
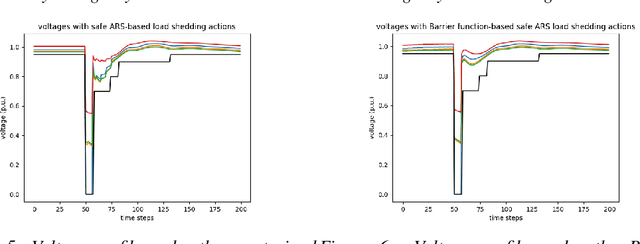
Under voltage load shedding has been considered as a standard approach to recover the voltage stability of the electric power grid under emergency conditions, yet this scheme usually trips a massive amount of load inefficiently. Reinforcement learning (RL) has been adopted as a promising approach to circumvent the issues; however, RL approach usually cannot guarantee the safety of the systems under control. In this paper, we discuss a couple of novel safe RL approaches, namely constrained optimization approach and Barrier function-based approach, that can safely recover voltage under emergency events. This method is general and can be applied to other safety-critical control problems. Numerical simulations on the 39-bus IEEE benchmark are performed to demonstrate the effectiveness of the proposed safe RL emergency control.

Scalable Voltage Control using Structure-Driven Hierarchical Deep Reinforcement Learning

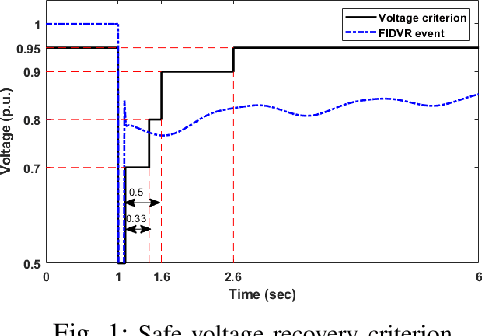
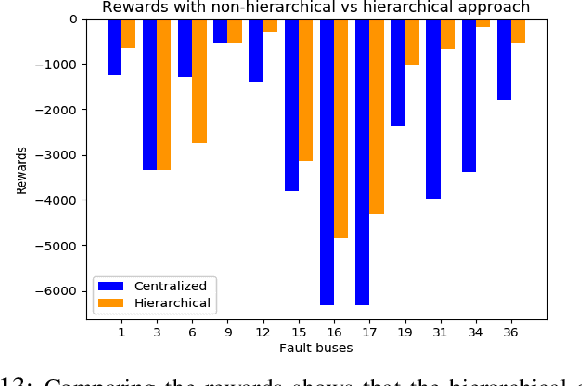
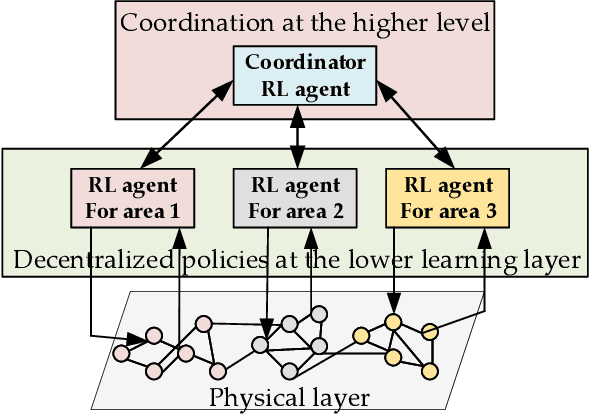
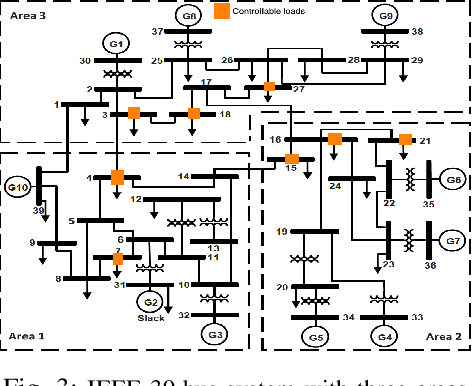
This paper presents a novel hierarchical deep reinforcement learning (DRL) based design for the voltage control of power grids. DRL agents are trained for fast, and adaptive selection of control actions such that the voltage recovery criterion can be met following disturbances. Existing voltage control techniques suffer from the issues of speed of operation, optimal coordination between different locations, and scalability. We exploit the area-wise division structure of the power system to propose a hierarchical DRL design that can be scaled to the larger grid models. We employ an enhanced augmented random search algorithm that is tailored for the voltage control problem in a two-level architecture. We train area-wise decentralized RL agents to compute lower-level policies for the individual areas, and concurrently train a higher-level DRL agent that uses the updates of the lower-level policies to efficiently coordinate the control actions taken by the lower-level agents. Numerical experiments on the IEEE benchmark 39-bus model with 3 areas demonstrate the advantages and various intricacies of the proposed hierarchical approach.

Imposing Robust Structured Control Constraint on Reinforcement Learning of Linear Quadratic Regulator

This paper discusses learning a structured feedback control to obtain sufficient robustness to exogenous inputs for linear dynamic systems with unknown state matrix. The structural constraint on the controller is necessary for many cyber-physical systems, and our approach presents a design for any generic structure, paving the way for distributed learning control. The ideas from reinforcement learning (RL) in conjunction with control-theoretic sufficient stability and performance guarantees are used to develop the methodology. First, a model-based framework is formulated using dynamic programming to embed the structural constraint in the linear quadratic regulator (LQR) setting along with sufficient robustness conditions. Thereafter, we translate these conditions to a data-driven learning-based framework - robust structured reinforcement learning (RSRL) that enjoys the control-theoretic guarantees on stability and convergence. We validate our theoretical results with a simulation on a multi-agent network with $6$ agents.

Reinforcement Learning of Structured Control for Linear Systems with Unknown State Matrix

This paper delves into designing stabilizing feedback control gains for continuous linear systems with unknown state matrix, in which the control is subject to a general structural constraint. We bring forth the ideas from reinforcement learning (RL) in conjunction with sufficient stability and performance guarantees in order to design these structured gains using the trajectory measurements of states and controls. We first formulate a model-based framework using dynamic programming (DP) to embed the structural constraint to the Linear Quadratic Regulator (LQR) gain computation in the continuous-time setting. Subsequently, we transform this LQR formulation into a policy iteration RL algorithm that can alleviate the requirement of known state matrix in conjunction with maintaining the feedback gain structure. Theoretical guarantees are provided for stability and convergence of the structured RL (SRL) algorithm. The introduced RL framework is general and can be applied to any control structure. A special control structure enabled by this RL framework is distributed learning control which is necessary for many large-scale cyber-physical systems. As such, we validate our theoretical results with numerical simulations on a multi-agent networked linear time-invariant (LTI) dynamic system.