Allegro-Legato: Scalable, Fast, and Robust Neural-Network Quantum Molecular Dynamics via Sharpness-Aware Minimization

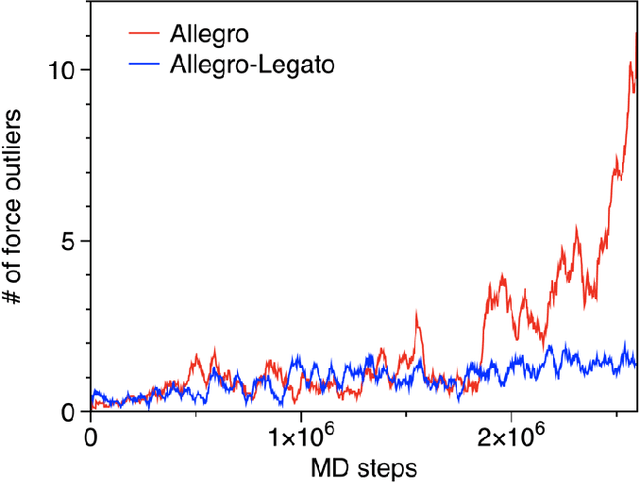
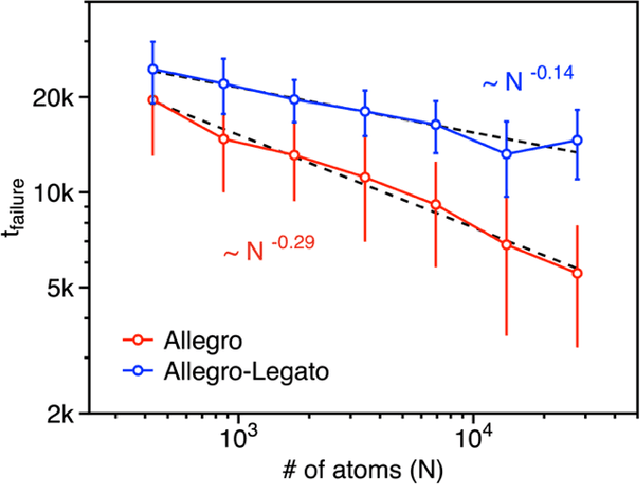
Neural-network quantum molecular dynamics (NNQMD) simulations based on machine learning are revolutionizing atomistic simulations of materials by providing quantum-mechanical accuracy but orders-of-magnitude faster, illustrated by ACM Gordon Bell prize (2020) and finalist (2021). State-of-the-art (SOTA) NNQMD model founded on group theory featuring rotational equivariance and local descriptors has provided much higher accuracy and speed than those models, thus named Allegro (meaning fast). On massively parallel supercomputers, however, it suffers a fidelity-scaling problem, where growing number of unphysical predictions of interatomic forces prohibits simulations involving larger numbers of atoms for longer times. Here, we solve this problem by combining the Allegro model with sharpness aware minimization (SAM) for enhancing the robustness of model through improved smoothness of the loss landscape. The resulting Allegro-Legato (meaning fast and "smooth") model was shown to elongate the time-to-failure $t_\textrm{failure}$, without sacrificing computational speed or accuracy. Specifically, Allegro-Legato exhibits much weaker dependence of timei-to-failure on the problem size, $t_{\textrm{failure}} \propto N^{-0.14}$ ($N$ is the number of atoms) compared to the SOTA Allegro model $\left(t_{\textrm{failure}} \propto N^{-0.29}\right)$, i.e., systematically delayed time-to-failure, thus allowing much larger and longer NNQMD simulations without failure. The model also exhibits excellent computational scalability and GPU acceleration on the Polaris supercomputer at Argonne Leadership Computing Facility. Such scalable, accurate, fast and robust NNQMD models will likely find broad applications in NNQMD simulations on emerging exaflop/s computers, with a specific example of accounting for nuclear quantum effects in the dynamics of ammonia.

Physics-informed Neural-Network Software for Molecular Dynamics Applications

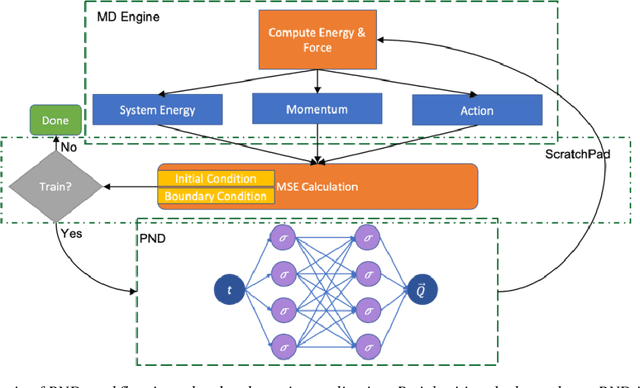
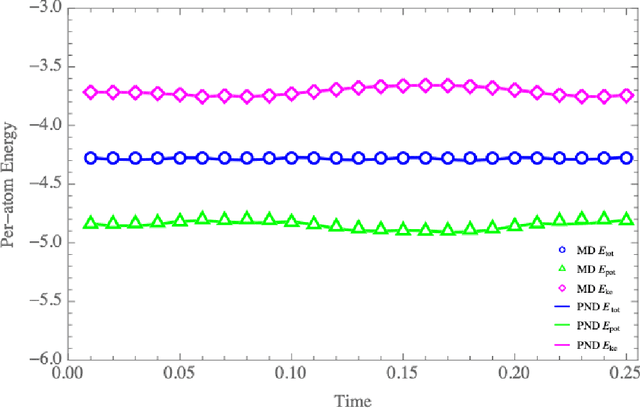
We have developed a novel differential equation solver software called PND based on the physics-informed neural network for molecular dynamics simulators. Based on automatic differentiation technique provided by Pytorch, our software allows users to flexibly implement equation of atom motions, initial and boundary conditions, and conservation laws as loss function to train the network. PND comes with a parallel molecular dynamics (MD) engine in order for users to examine and optimize loss function design, and different conservation laws and boundary conditions, and hyperparameters, thereby accelerate the PINN-based development for molecular applications.