Allegro-Legato: Scalable, Fast, and Robust Neural-Network Quantum Molecular Dynamics via Sharpness-Aware Minimization

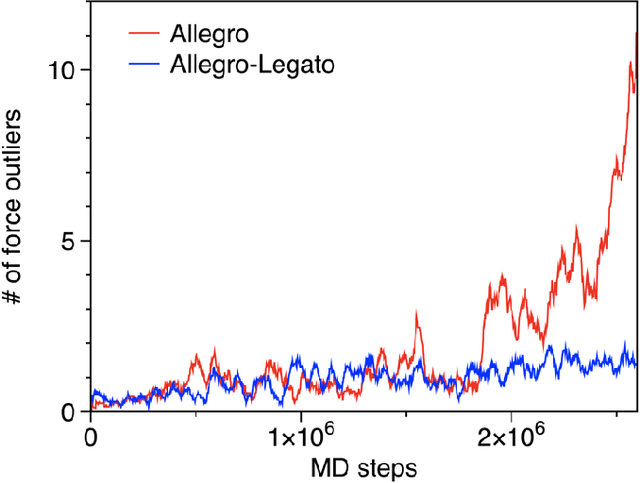
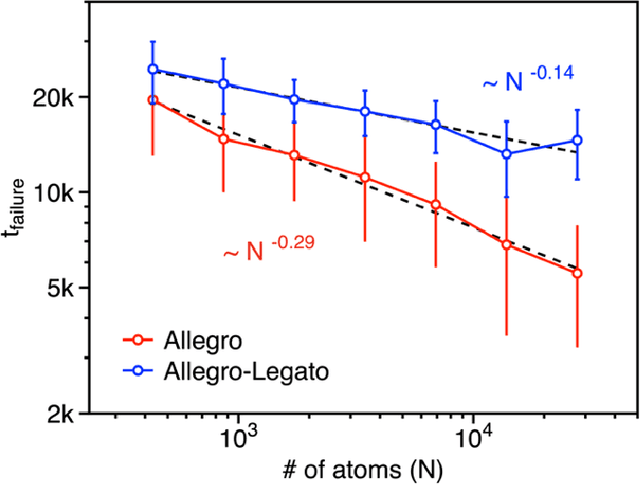
Neural-network quantum molecular dynamics (NNQMD) simulations based on machine learning are revolutionizing atomistic simulations of materials by providing quantum-mechanical accuracy but orders-of-magnitude faster, illustrated by ACM Gordon Bell prize (2020) and finalist (2021). State-of-the-art (SOTA) NNQMD model founded on group theory featuring rotational equivariance and local descriptors has provided much higher accuracy and speed than those models, thus named Allegro (meaning fast). On massively parallel supercomputers, however, it suffers a fidelity-scaling problem, where growing number of unphysical predictions of interatomic forces prohibits simulations involving larger numbers of atoms for longer times. Here, we solve this problem by combining the Allegro model with sharpness aware minimization (SAM) for enhancing the robustness of model through improved smoothness of the loss landscape. The resulting Allegro-Legato (meaning fast and "smooth") model was shown to elongate the time-to-failure $t_\textrm{failure}$, without sacrificing computational speed or accuracy. Specifically, Allegro-Legato exhibits much weaker dependence of timei-to-failure on the problem size, $t_{\textrm{failure}} \propto N^{-0.14}$ ($N$ is the number of atoms) compared to the SOTA Allegro model $\left(t_{\textrm{failure}} \propto N^{-0.29}\right)$, i.e., systematically delayed time-to-failure, thus allowing much larger and longer NNQMD simulations without failure. The model also exhibits excellent computational scalability and GPU acceleration on the Polaris supercomputer at Argonne Leadership Computing Facility. Such scalable, accurate, fast and robust NNQMD models will likely find broad applications in NNQMD simulations on emerging exaflop/s computers, with a specific example of accounting for nuclear quantum effects in the dynamics of ammonia.

Quasi-potential theory for escape problem: Quantitative sharpness effect on SGD's escape from local minima

We develop a quantitative theory on an escape problem of a stochastic gradient descent (SGD) algorithm and investigate the effect of sharpness of loss surfaces on the escape. Deep learning has achieved tremendous success in various domains, however, it has opened up various theoretical open questions. One of the typical questions is why an SGD can find parameters that generalize well over non-convex loss surfaces. An escape problem is an approach to tackle this question, which investigates how efficiently an SGD escapes from local minima. In this paper, we develop a quasi-potential theory for the escape problem, by applying a theory of stochastic dynamical systems. We show that the quasi-potential theory can handle both geometric properties of loss surfaces and a covariance structure of gradient noise in a unified manner, while they have been separately studied in previous works. Our theoretical results imply that (i) the sharpness of loss surfaces contributes to the slow escape of an SGD, and (ii) the SGD's noise structure cancels the effect and exponentially accelerates the escape. We also conduct experiments to empirically validate our theory using neural networks trained with real data.

Minimum sharpness: Scale-invariant parameter-robustness of neural networks

Toward achieving robust and defensive neural networks, the robustness against the weight parameters perturbations, i.e., sharpness, attracts attention in recent years (Sun et al., 2020). However, sharpness is known to remain a critical issue, "scale-sensitivity." In this paper, we propose a novel sharpness measure, Minimum Sharpness. It is known that NNs have a specific scale transformation that constitutes equivalent classes where functional properties are completely identical, and at the same time, their sharpness could change unlimitedly. We define our sharpness through a minimization problem over the equivalent NNs being invariant to the scale transformation. We also develop an efficient and exact technique to make the sharpness tractable, which reduces the heavy computational costs involved with Hessian. In the experiment, we observed that our sharpness has a valid correlation with the generalization of NNs and runs with less computational cost than existing sharpness measures.