Takuya Kanazawa
Multivariate Uncertainty Quantification with Tomographic Quantile Forests
Dec 18, 2025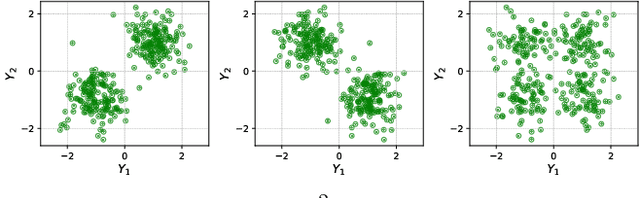
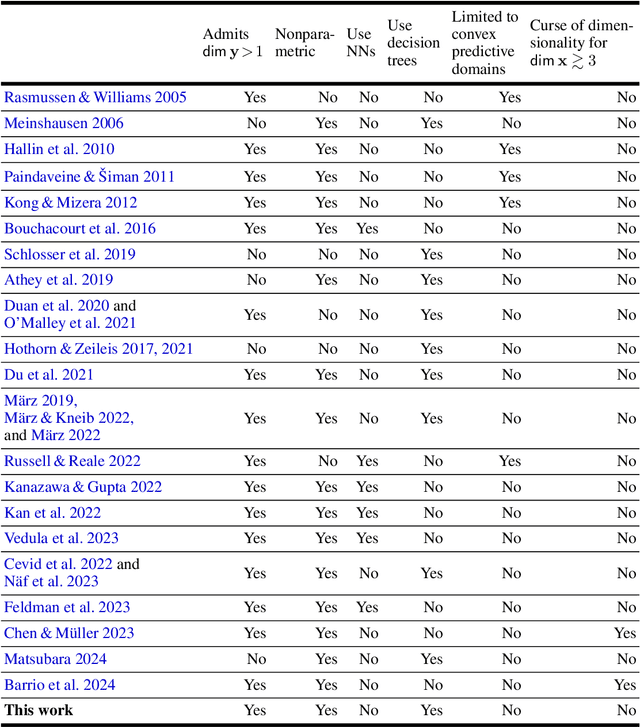
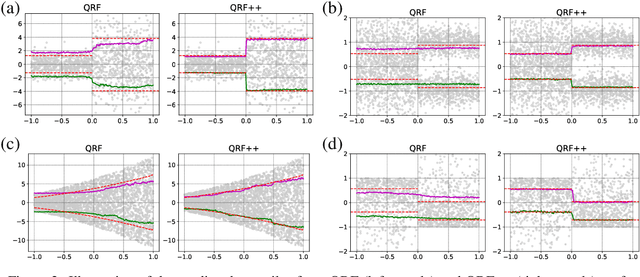
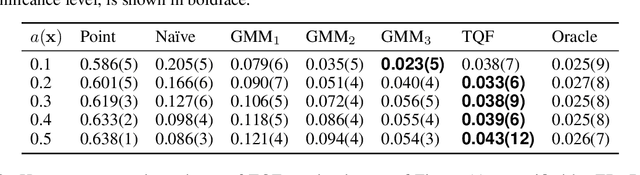
Abstract:Quantifying predictive uncertainty is essential for safe and trustworthy real-world AI deployment. Yet, fully nonparametric estimation of conditional distributions remains challenging for multivariate targets. We propose Tomographic Quantile Forests (TQF), a nonparametric, uncertainty-aware, tree-based regression model for multivariate targets. TQF learns conditional quantiles of directional projections $\mathbf{n}^{\top}\mathbf{y}$ as functions of the input $\mathbf{x}$ and the unit direction $\mathbf{n}$. At inference, it aggregates quantiles across many directions and reconstructs the multivariate conditional distribution by minimizing the sliced Wasserstein distance via an efficient alternating scheme with convex subproblems. Unlike classical directional-quantile approaches that typically produce only convex quantile regions and require training separate models for different directions, TQF covers all directions with a single model without imposing convexity restrictions. We evaluate TQF on synthetic and real-world datasets, and release the source code on GitHub.
Latent-Conditioned Policy Gradient for Multi-Objective Deep Reinforcement Learning
Mar 15, 2023Abstract:Sequential decision making in the real world often requires finding a good balance of conflicting objectives. In general, there exist a plethora of Pareto-optimal policies that embody different patterns of compromises between objectives, and it is technically challenging to obtain them exhaustively using deep neural networks. In this work, we propose a novel multi-objective reinforcement learning (MORL) algorithm that trains a single neural network via policy gradient to approximately obtain the entire Pareto set in a single run of training, without relying on linear scalarization of objectives. The proposed method works in both continuous and discrete action spaces with no design change of the policy network. Numerical experiments in benchmark environments demonstrate the practicality and efficacy of our approach in comparison to standard MORL baselines.
Sample-based Uncertainty Quantification with a Single Deterministic Neural Network
Sep 17, 2022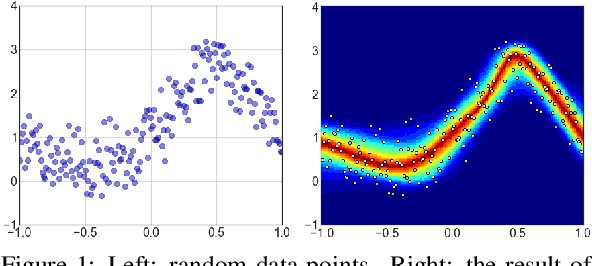
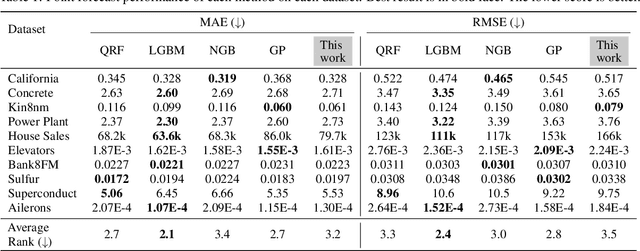
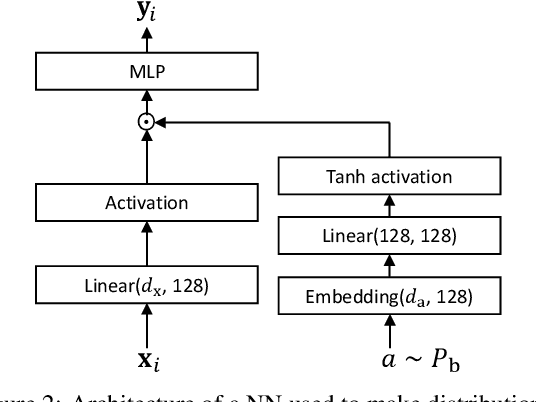
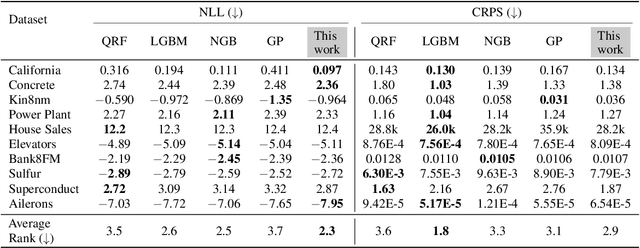
Abstract:Development of an accurate, flexible, and numerically efficient uncertainty quantification (UQ) method is one of fundamental challenges in machine learning. Previously, a UQ method called DISCO Nets has been proposed (Bouchacourt et al., 2016) that trains a neural network by minimizing the so-called energy score on training data. This method has shown superior performance on a hand pose estimation task in computer vision, but it remained unclear whether this method works as nicely for regression on tabular data, and how it competes with more recent advanced UQ methods such as NGBoost. In this paper, we propose an improved neural architecture of DISCO Nets that admits a more stable and smooth training. We benchmark this approach on miscellaneous real-world tabular datasets and confirm that it is competitive with or even superior to standard UQ baselines. We also provide a new elementary proof for the validity of using the energy score to learn predictive distributions. Further, we point out that DISCO Nets in its original form ignore epistemic uncertainty and only capture aleatoric uncertainty. We propose a simple fix to this problem.
Distributional Actor-Critic Ensemble for Uncertainty-Aware Continuous Control
Jul 27, 2022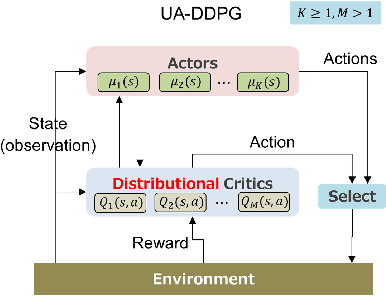
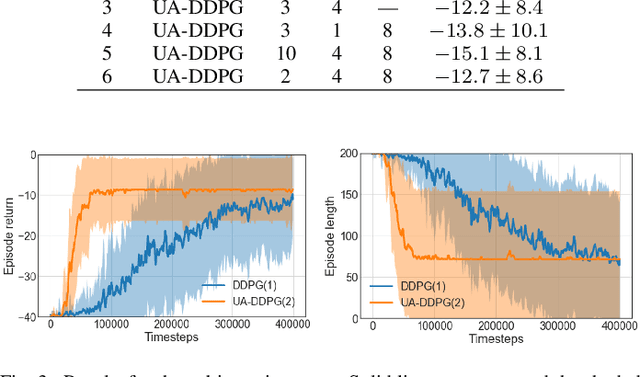
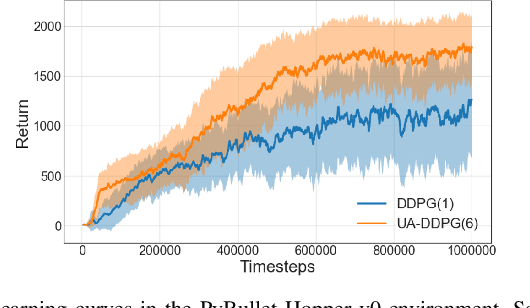
Abstract:Uncertainty quantification is one of the central challenges for machine learning in real-world applications. In reinforcement learning, an agent confronts two kinds of uncertainty, called epistemic uncertainty and aleatoric uncertainty. Disentangling and evaluating these uncertainties simultaneously stands a chance of improving the agent's final performance, accelerating training, and facilitating quality assurance after deployment. In this work, we propose an uncertainty-aware reinforcement learning algorithm for continuous control tasks that extends the Deep Deterministic Policy Gradient algorithm (DDPG). It exploits epistemic uncertainty to accelerate exploration and aleatoric uncertainty to learn a risk-sensitive policy. We conduct numerical experiments showing that our variant of DDPG outperforms vanilla DDPG without uncertainty estimation in benchmark tasks on robotic control and power-grid optimization.
One-parameter family of acquisition functions for efficient global optimization
Apr 26, 2021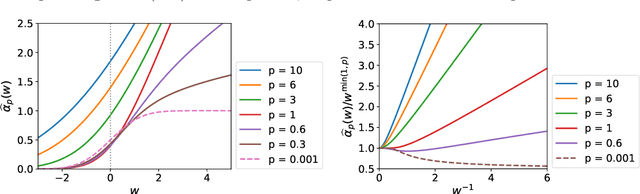
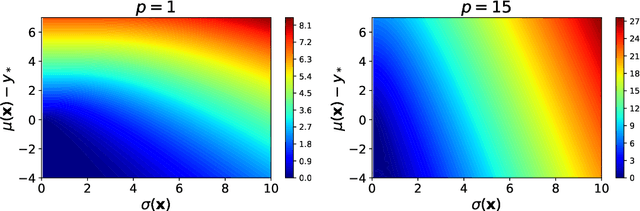
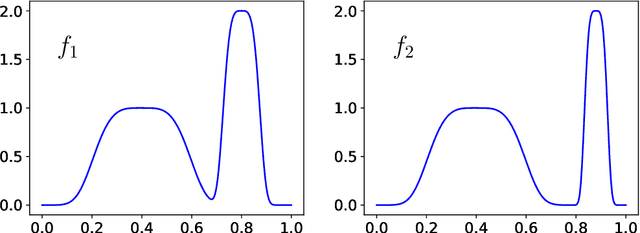
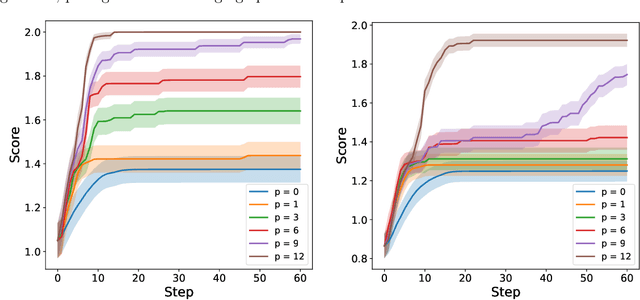
Abstract:Bayesian optimization (BO) with Gaussian processes is a powerful methodology to optimize an expensive black-box function with as few function evaluations as possible. The expected improvement (EI) and probability of improvement (PI) are among the most widely used schemes for BO. There is a plethora of other schemes that outperform EI and PI, but most of them are numerically far more expensive than EI and PI. In this work, we propose a new one-parameter family of acquisition functions for BO that unifies EI and PI. The proposed method is numerically inexpensive, is easy to implement, can be easily parallelized, and on benchmark tasks shows a performance superior to EI and GP-UCB. Its generalization to BO with Student-t processes is also presented.
Efficient Bayesian Optimization using Multiscale Graph Correlation
Mar 17, 2021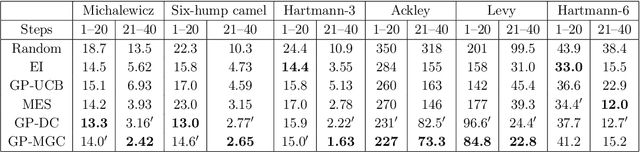
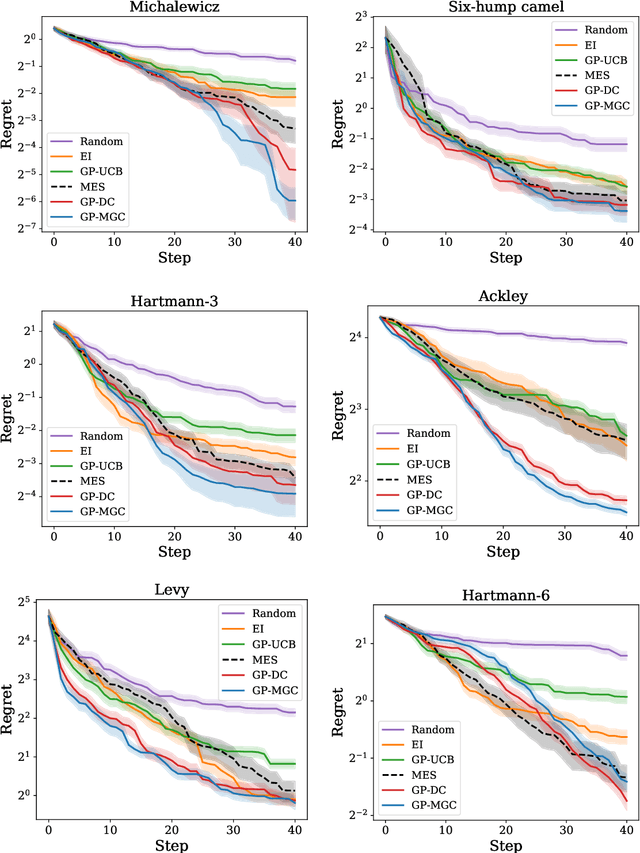
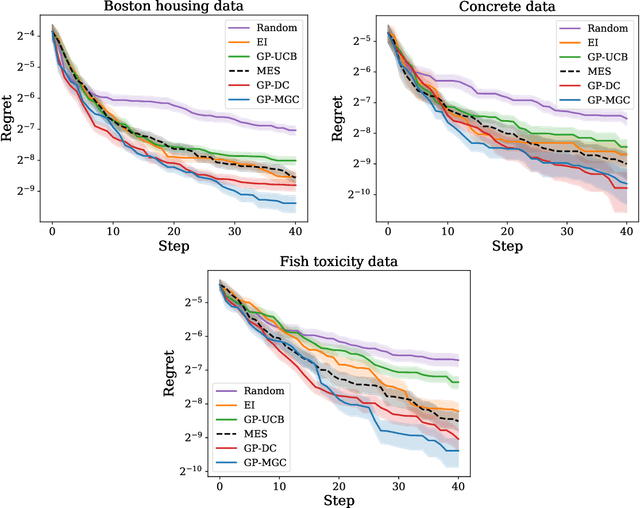
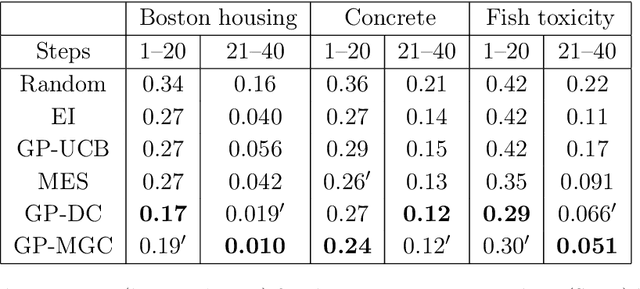
Abstract:Bayesian optimization is a powerful tool to optimize a black-box function, the evaluation of which is time-consuming or costly. In this paper, we propose a new approach to Bayesian optimization called GP-MGC, which maximizes multiscale graph correlation with respect to the global maximum to determine the next query point. We present our evaluation of GP-MGC in applications involving both synthetic benchmark functions and real-world datasets and demonstrate that GP-MGC performs as well as or even better than state-of-the-art methods such as max-value entropy search and GP-UCB.
Using Distance Correlation for Efficient Bayesian Optimization
Feb 17, 2021
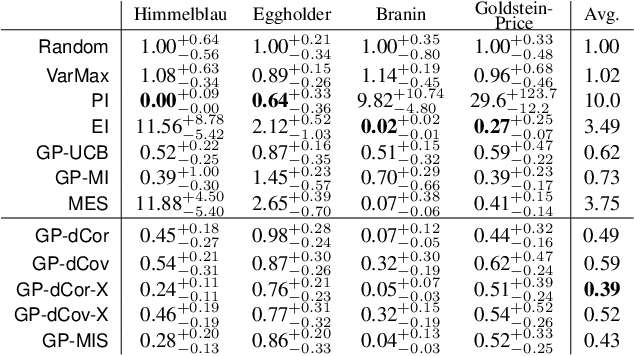
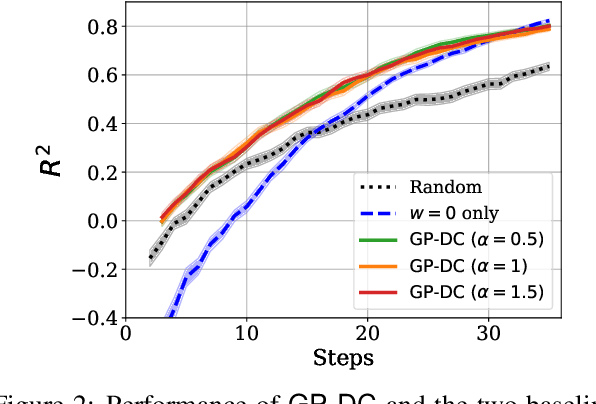
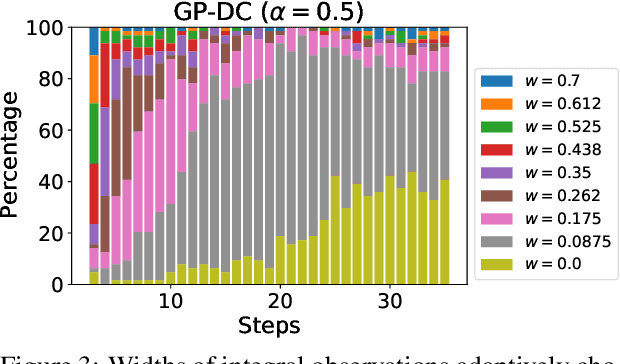
Abstract:We propose a novel approach for Bayesian optimization, called $\textsf{GP-DC}$, which combines Gaussian processes with distance correlation. It balances exploration and exploitation automatically, and requires no manual parameter tuning. We evaluate $\textsf{GP-DC}$ on a number of benchmark functions and observe that it outperforms state-of-the-art methods such as $\textsf{GP-UCB}$ and max-value entropy search, as well as the classical expected improvement heuristic. We also apply $\textsf{GP-DC}$ to optimize sequential integral observations with a variable integration range and verify its empirical efficiency on both synthetic and real-world datasets.
Accelerating small-angle scattering experiments with simulation-based machine learning
Aug 24, 2019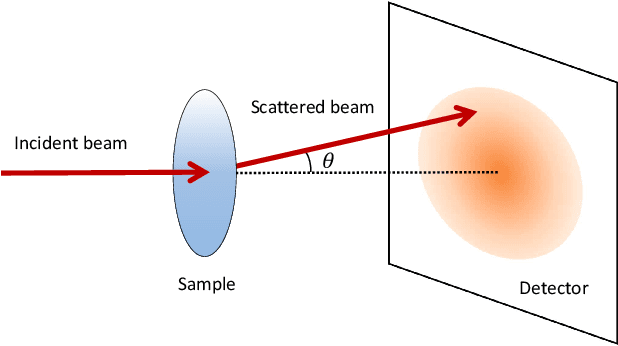

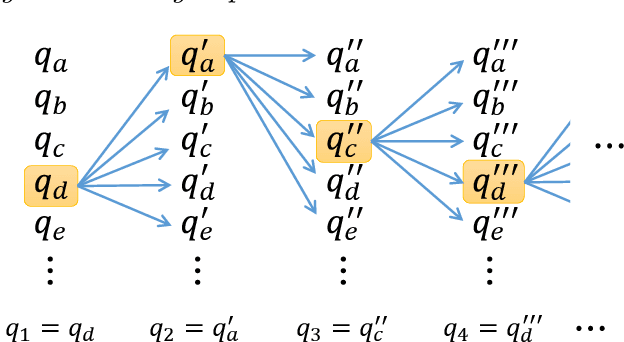
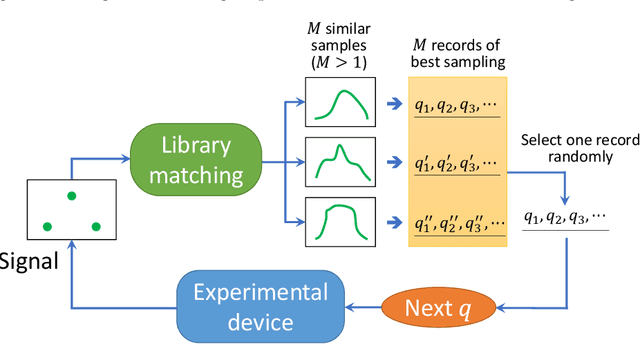
Abstract:Making material experiments more efficient is a high priority for materials scientists who seek to discover new materials with desirable properties. In this paper, we investigate how to optimize the laborious sequential measurements of materials properties with data-driven methods, taking the small-angle neutron scattering (SANS) experiment as a test case. We propose two methods for optimizing sequential data sampling. These methods iteratively suggest the best target for the next measurement by performing a statistical analysis of the already acquired data, so that maximal information is gained at each step of an experiment. We conducted numerical simulations of SANS experiments for virtual materials and confirmed that the proposed methods significantly outperform baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge