One-parameter family of acquisition functions for efficient global optimization
Paper and Code
Apr 26, 2021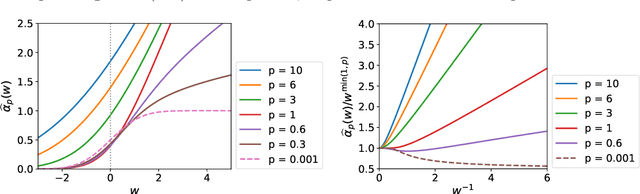
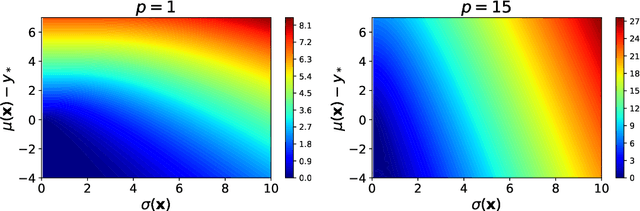
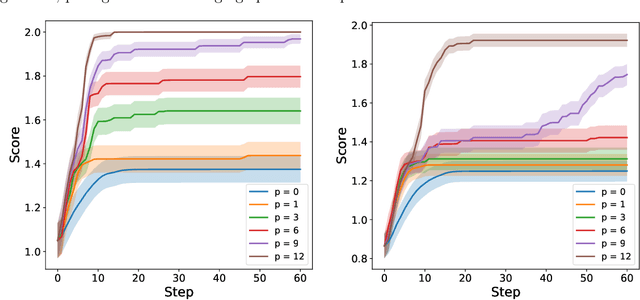
Bayesian optimization (BO) with Gaussian processes is a powerful methodology to optimize an expensive black-box function with as few function evaluations as possible. The expected improvement (EI) and probability of improvement (PI) are among the most widely used schemes for BO. There is a plethora of other schemes that outperform EI and PI, but most of them are numerically far more expensive than EI and PI. In this work, we propose a new one-parameter family of acquisition functions for BO that unifies EI and PI. The proposed method is numerically inexpensive, is easy to implement, can be easily parallelized, and on benchmark tasks shows a performance superior to EI and GP-UCB. Its generalization to BO with Student-t processes is also presented.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge