Using Distance Correlation for Efficient Bayesian Optimization
Paper and Code
Feb 17, 2021
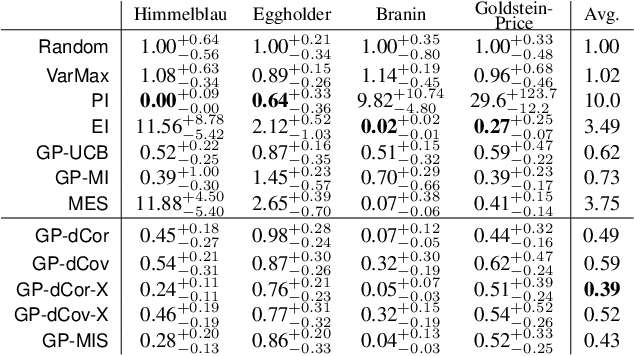
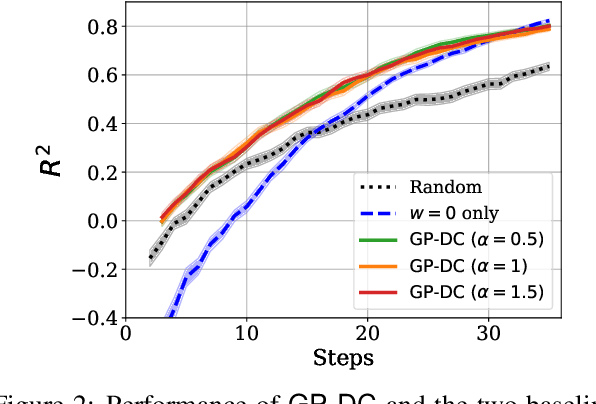
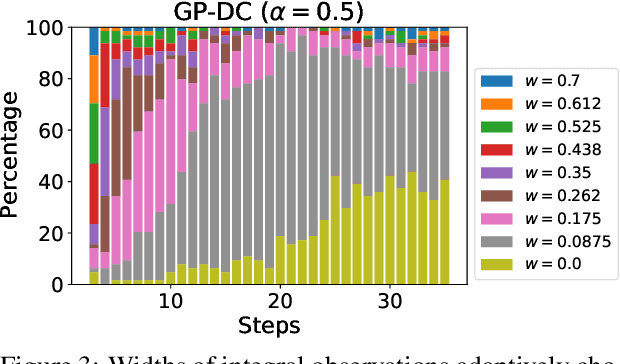
We propose a novel approach for Bayesian optimization, called $\textsf{GP-DC}$, which combines Gaussian processes with distance correlation. It balances exploration and exploitation automatically, and requires no manual parameter tuning. We evaluate $\textsf{GP-DC}$ on a number of benchmark functions and observe that it outperforms state-of-the-art methods such as $\textsf{GP-UCB}$ and max-value entropy search, as well as the classical expected improvement heuristic. We also apply $\textsf{GP-DC}$ to optimize sequential integral observations with a variable integration range and verify its empirical efficiency on both synthetic and real-world datasets.
* 10 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge