Fast Data-driven Greedy Sensor Selection for Ridge Regression

We propose a data-driven sensor-selection algorithm for accurate estimation of the target variables from the selected measurements. The target variables are assumed to be estimated by a ridge-regression estimator which is trained based on the data. The proposed algorithm greedily selects sensors for minimization of the cost function of the estimator. Sensor selection which prevents the overfitting of the resulting estimator can be realized by setting a positive regularization parameter. The greedy solution is computed in quite a short time by using some recurrent relations that we derive. Furthermore, we show that sensor selection can be accelerated by dimensionality reduction of the target variables without large deterioration of the estimation performance. The effectiveness of the proposed algorithm is verified for two real-world datasets. The first dataset is a dataset of sea surface temperature for sensor selection for reconstructing large data, and the second is a dataset of surface pressure distribution and yaw angle of a ground vehicle for sensor selection for estimation. The experiments reveal that the proposed algorithm outperforms some data-drive selection algorithms including the orthogonal matching pursuit.

Seismic Wavefield Reconstruction based on Compressed Sensing using Data-Driven Reduced-Order Model

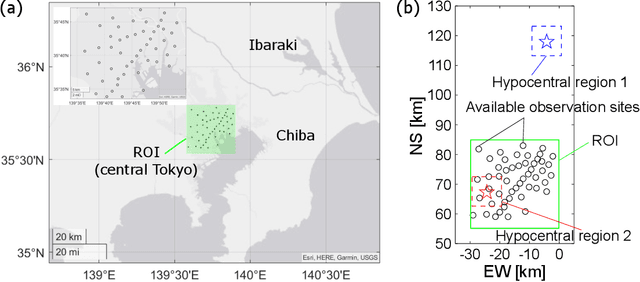
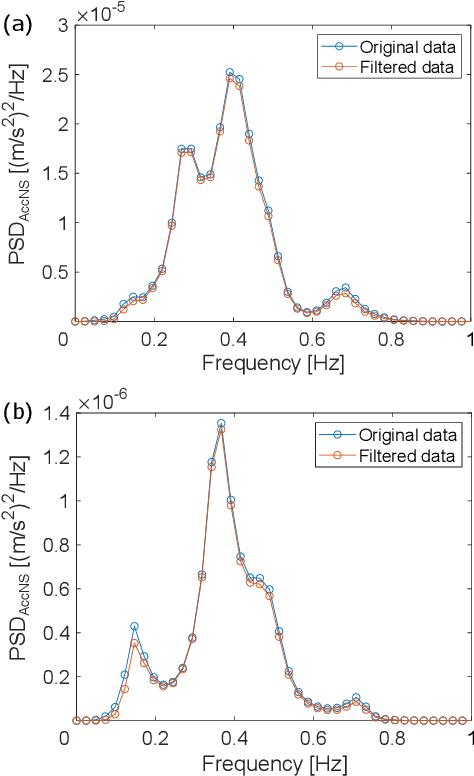
A seismic wavefield reconstruction framework based on compressed sensing using the data-driven reduced-order model (ROM) is proposed and its characteristics are investigated through numerical experiments. The data-driven ROM is generated from the dataset of the wavefield using the singular value decomposition. The spatially continuous seismic wavefield is reconstructed from the sparse and discrete observation and the data-driven ROM. The observation sites used for reconstruction are effectively selected by the sensor optimization method for linear inverse problems based on a greedy algorithm. The validity of the proposed method was confirmed by the reconstruction based on the noise-free observation. Since the ROM of the wavefield is used as prior information, the reconstruction error is reduced to an approximately lower error bound of the present framework, even though the number of sensors used for reconstruction is limited and randomly selected. In addition, the reconstruction error obtained by the proposed framework is much smaller than that obtained by the Gaussian process regression. For the numerical experiment with noise-contaminated observation, the reconstructed wavefield is degraded due to the observation noise, but the reconstruction error obtained by the present framework with all available observation sites is close to a lower error bound, even though the reconstructed wavefield using the Gaussian process regression is fully collapsed. Although the reconstruction error is larger than that obtained using all observation sites, the number of observation sites used for reconstruction can be reduced while minimizing the deterioration and scatter of the reconstructed data by combining it with the sensor optimization method.

Observation Site Selection for Physical Model Parameter Estimation toward Process-Driven Seismic Wavefield Reconstruction

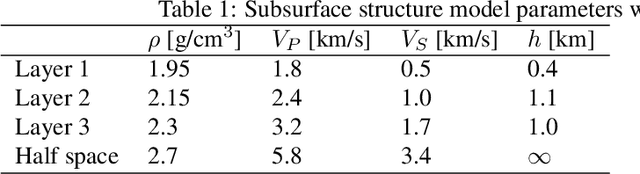
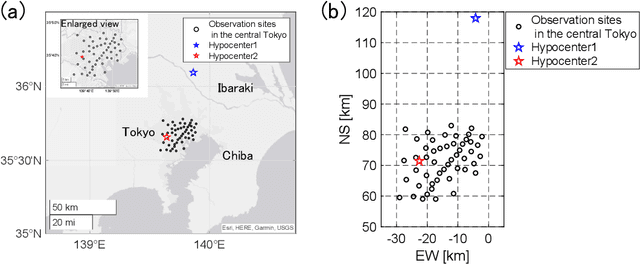
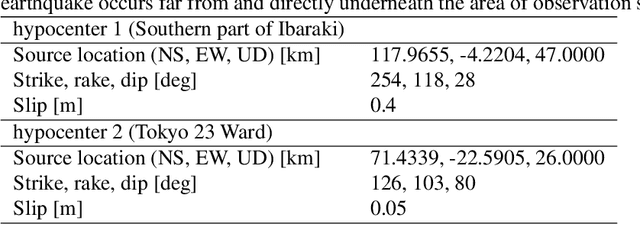
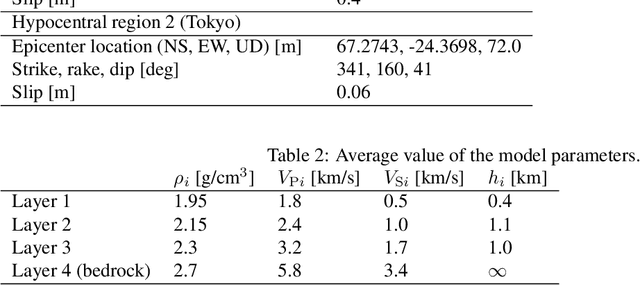
The seismic data not only acquired by seismometers but also acquired by vibrometers installed in buildings and infrastructure and accelerometers installed in smartphones will be certainly utilized for seismic research in the near future. Since it is impractical to utilize all the seismic big data in terms of the computational cost, methods which can select observation sites depending on the purpose are indispensable. We propose an observation site selection method for the accurate reconstruction of the seismic wavefield by process-driven approaches. The proposed method selects observation sites suitable for accurately estimating physical model parameters such as subsurface structures and source information to be input into a numerical simulation of the seismic wavefield. The seismic wavefield is reconstructed by the numerical simulation using the parameters estimated based on the observed signals at only observation sites selected by the proposed method. The observation site selection in the proposed method is based on the sensitivity of each observation site candidate to the physical model parameters; the matrix corresponding to the sensitivity is constructed by approximately calculating the derivatives based on the simulations, and then, observation sites are selected by evaluating the quantity of the sensitivity matrix based on the D-optimality criterion proposed in the optimal design of experiments. In the present study, physical knowledge on the sensitivity to the parameters such as seismic velocity, layer thickness, and hypocenter location was obtained by investigating the characteristics of the sensitivity matrix. Furthermore, the effectiveness of the proposed method was shown by verifying the accuracy of seismic wavefield reconstruction using the observation sites selected by the proposed method.

Data-Driven Sensor Selection Method Based on Proximal Optimization for High-Dimensional Data With Correlated Measurement Noise

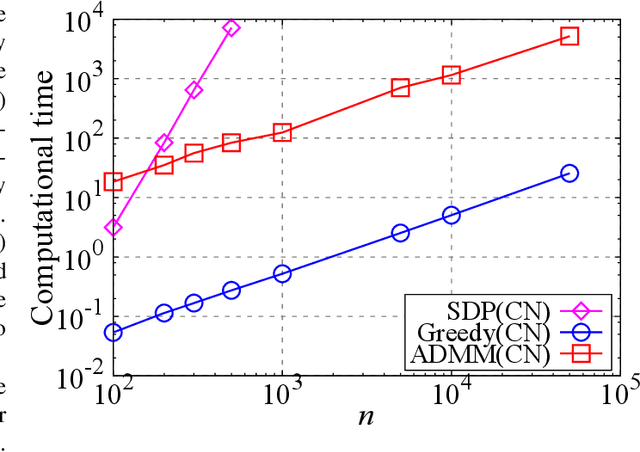
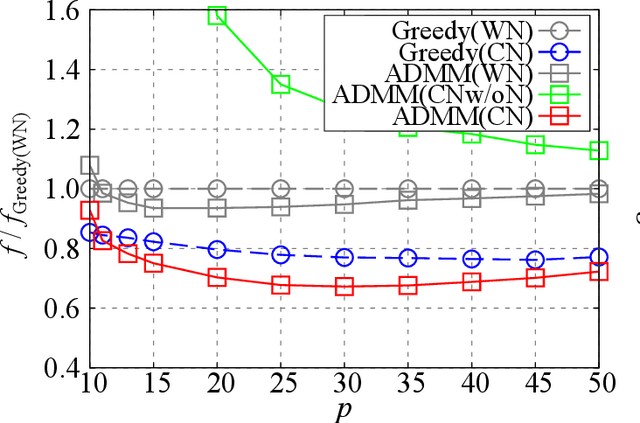
The present paper proposes a data-driven sensor selection method for a high-dimensional nondynamical system with strongly correlated measurement noise. The proposed method is based on proximal optimization and determines sensor locations by minimizing the trace of the inverse of the Fisher information matrix under a block-sparsity hard constraint. The proposed method can avoid the difficulty of sensor selection with strongly correlated measurement noise, in which the possible sensor locations must be known in advance for calculating the precision matrix for selecting sensor locations. The problem can be efficiently solved by the alternating direction method of multipliers, and the computational complexity of the proposed method is proportional to the number of potential sensor locations when it is used in combination with a low-rank expression of the measurement noise model. The advantage of the proposed method over existing sensor selection methods is demonstrated through experiments using artificial and real datasets.

Randomized Group-Greedy Method for Data-Driven Sensor Selection

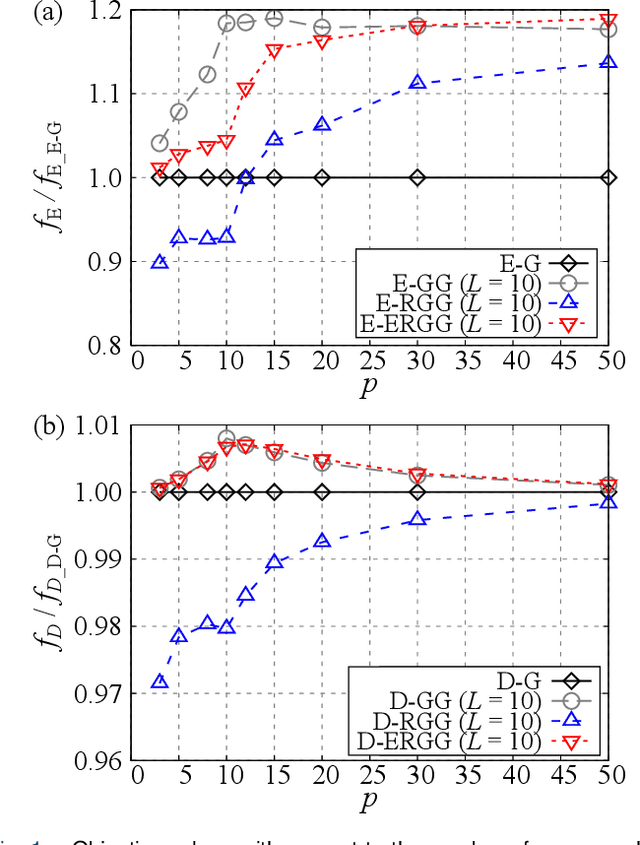
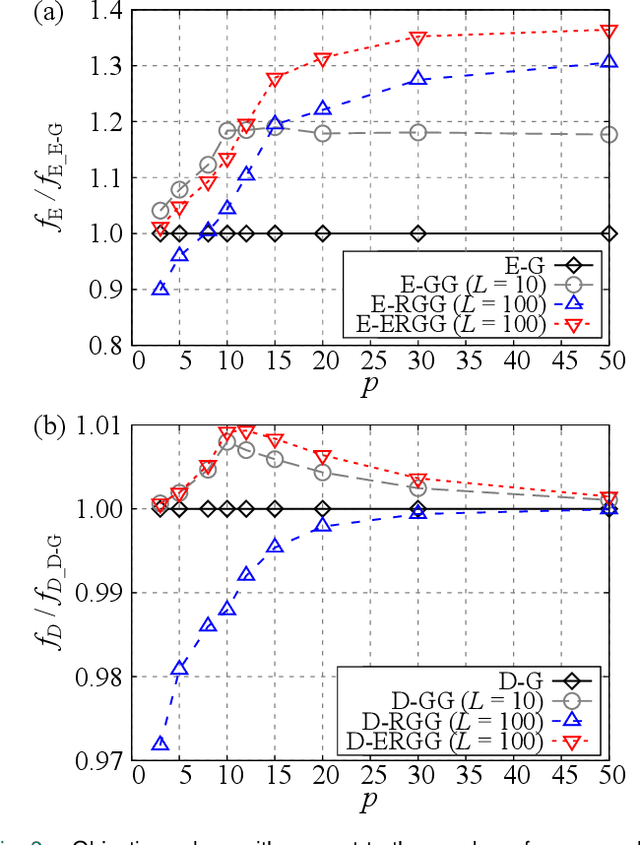
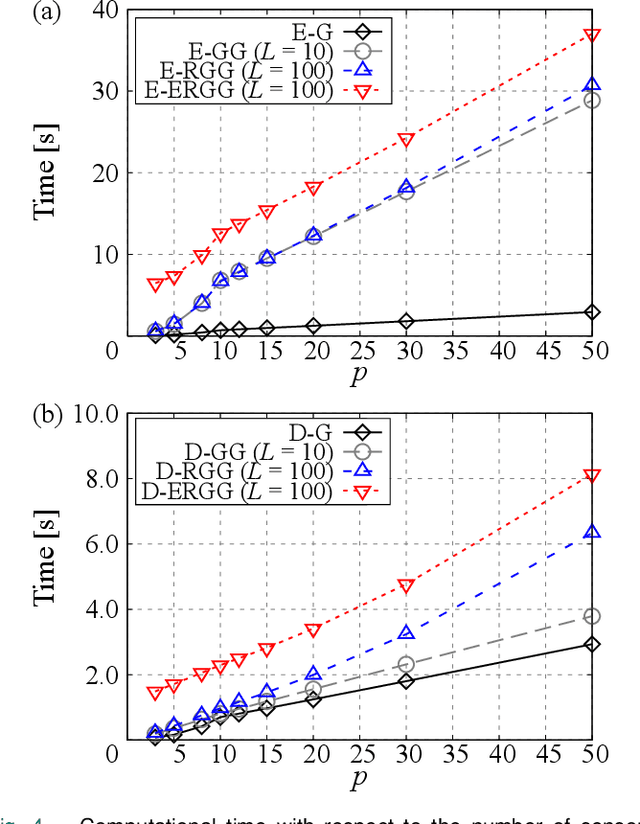
Randomized group-greedy methods for sensor selection problems are proposed. The randomized greedy sensor selection algorithm is straightforwardly applied to the group-greedy method, and a customized method is also considered. In the customized method, a part of the shrunken sensor candidates is selected to be the oversampled sensors by the common greedy method, and this strategy compensates for the deterioration of the solution due to shrunken sensor candidates. The proposed methods are implemented based on the D- and E-optimal design of experiments, and a numerical experiment is conducted using a randomly generated dataset. The proposed method can provide better optimization results than those obtained by the original group-greedy method when a similar computational cost is spent as for the original group-greedy method. This is because the group size for the group-greedy method can be increased as a result of the reduced sensor candidates by the randomized algorithm.

Nondominated-Solution-based Multiobjective-Greedy Sensor Selection for Optimal Design of Experiments

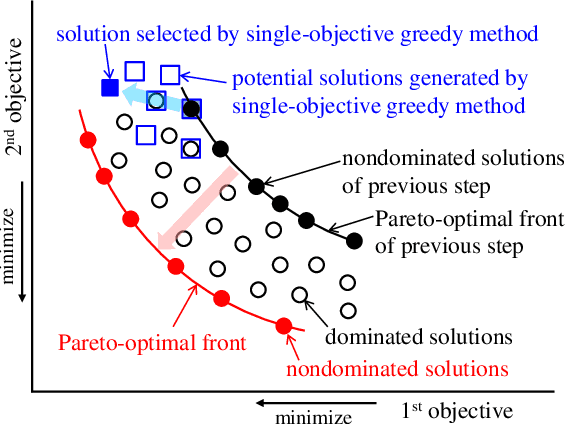
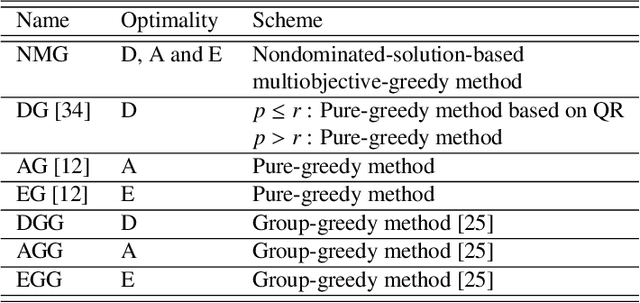
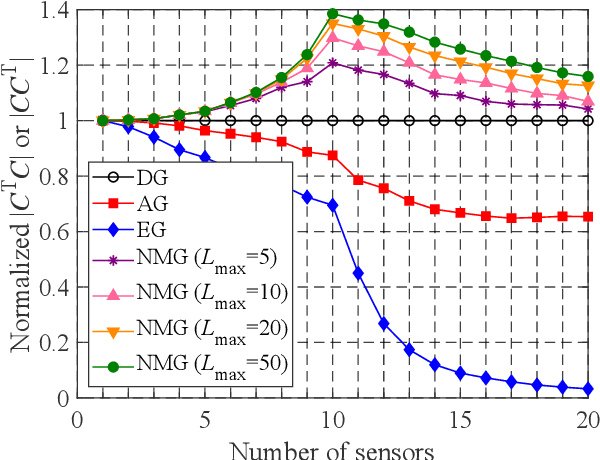
In this study, a nondominated-solution-based multiobjective-greedy sensor selection method for the optimal design of experiments is proposed and its performance is investigated. The proposed method simultaneously considers D-, A- and E-optimality and applies the idea of Pareto ranking to select the sensor set. With the proposed method, a new sensor is iteratively added to the nondominated solutions of sensor sets, and the multiobjective functions are evaluated for new sets of sensors based on increments in the relevant optimality index. The nondominated solutions are selected from the examined solutions, and the next sensor sets are then considered. With this procedure, the multiobjective optimization of sensor selection can be conducted with reasonable computational costs. The results show that the proposed method not only gives the Pareto-optimal front of the multiobjective optimization problem but also produces sets of sensors in terms of D-, A- and E-optimality, that are superior to the sets selected by pure-greedy methods that consider only a single objective function.