Data-Driven Sensor Selection Method Based on Proximal Optimization for High-Dimensional Data With Correlated Measurement Noise
Paper and Code
May 12, 2022
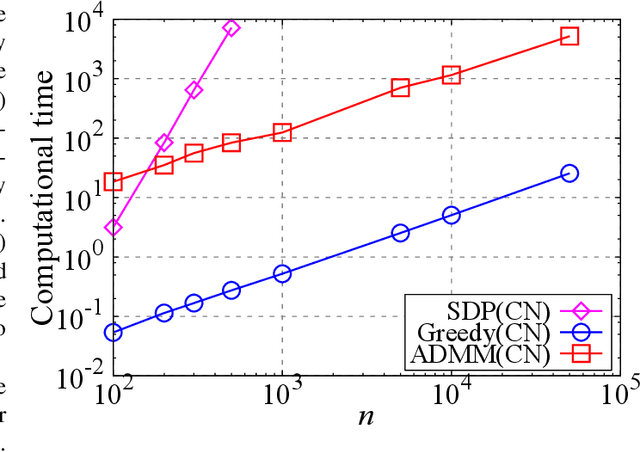

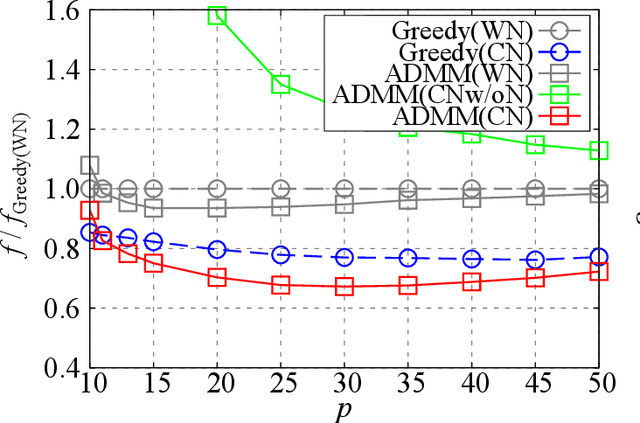
The present paper proposes a data-driven sensor selection method for a high-dimensional nondynamical system with strongly correlated measurement noise. The proposed method is based on proximal optimization and determines sensor locations by minimizing the trace of the inverse of the Fisher information matrix under a block-sparsity hard constraint. The proposed method can avoid the difficulty of sensor selection with strongly correlated measurement noise, in which the possible sensor locations must be known in advance for calculating the precision matrix for selecting sensor locations. The problem can be efficiently solved by the alternating direction method of multipliers, and the computational complexity of the proposed method is proportional to the number of potential sensor locations when it is used in combination with a low-rank expression of the measurement noise model. The advantage of the proposed method over existing sensor selection methods is demonstrated through experiments using artificial and real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge