Seismic Wavefield Reconstruction based on Compressed Sensing using Data-Driven Reduced-Order Model

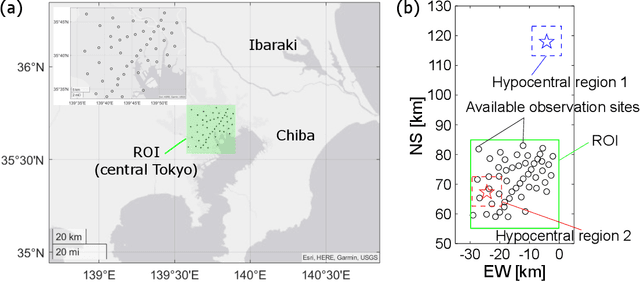
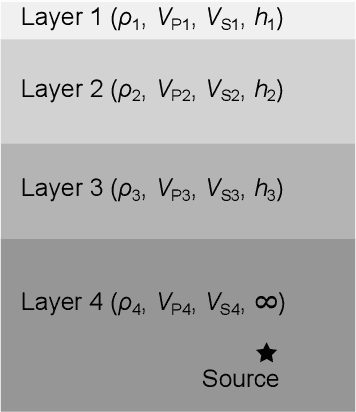
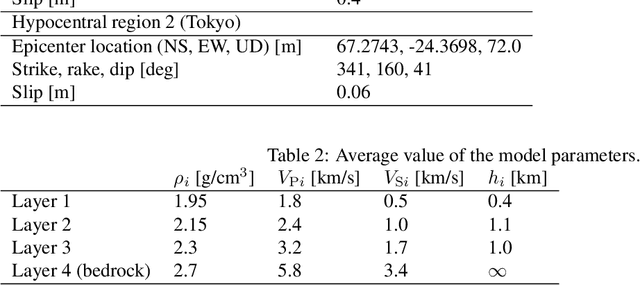
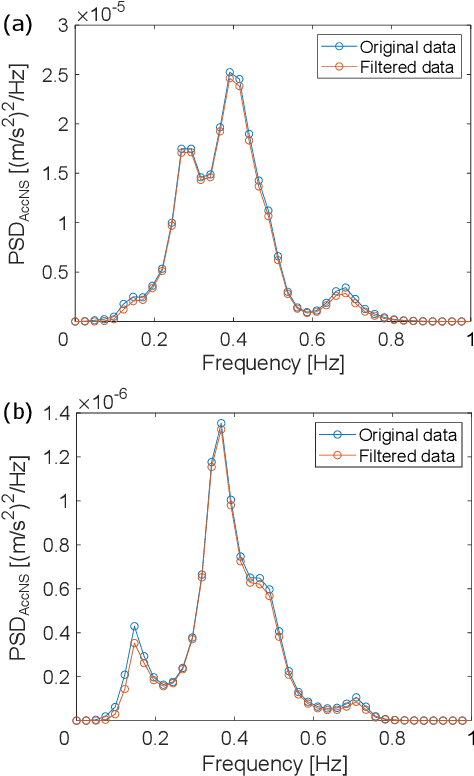
A seismic wavefield reconstruction framework based on compressed sensing using the data-driven reduced-order model (ROM) is proposed and its characteristics are investigated through numerical experiments. The data-driven ROM is generated from the dataset of the wavefield using the singular value decomposition. The spatially continuous seismic wavefield is reconstructed from the sparse and discrete observation and the data-driven ROM. The observation sites used for reconstruction are effectively selected by the sensor optimization method for linear inverse problems based on a greedy algorithm. The validity of the proposed method was confirmed by the reconstruction based on the noise-free observation. Since the ROM of the wavefield is used as prior information, the reconstruction error is reduced to an approximately lower error bound of the present framework, even though the number of sensors used for reconstruction is limited and randomly selected. In addition, the reconstruction error obtained by the proposed framework is much smaller than that obtained by the Gaussian process regression. For the numerical experiment with noise-contaminated observation, the reconstructed wavefield is degraded due to the observation noise, but the reconstruction error obtained by the present framework with all available observation sites is close to a lower error bound, even though the reconstructed wavefield using the Gaussian process regression is fully collapsed. Although the reconstruction error is larger than that obtained using all observation sites, the number of observation sites used for reconstruction can be reduced while minimizing the deterioration and scatter of the reconstructed data by combining it with the sensor optimization method.