Seismic-phase detection using multiple deep learning models for global and local representations of waveforms

The detection of earthquakes is a fundamental prerequisite for seismology and contributes to various research areas, such as forecasting earthquakes and understanding the crust/mantle structure. Recent advances in machine learning technologies have enabled the automatic detection of earthquakes from waveform data. In particular, various state-of-the-art deep-learning methods have been applied to this endeavour. In this study, we proposed and tested a novel phase detection method employing deep learning, which is based on a standard convolutional neural network in a new framework. The novelty of the proposed method is its separate explicit learning strategy for global and local representations of waveforms, which enhances its robustness and flexibility. Prior to modelling the proposed method, we identified local representations of the waveform by the multiple clustering of waveforms, in which the data points were optimally partitioned. Based on this result, we considered a global representation and two local representations of the waveform. Subsequently, different phase detection models were trained for each global and local representation. For a new waveform, the overall phase probability was evaluated as a product of the phase probabilities of each model. This additional information on local representations makes the proposed method robust to noise, which is demonstrated by its application to the test data. Furthermore, an application to seismic swarm data demonstrated the robust performance of the proposed method compared with those of other deep learning methods. Finally, in an application to low-frequency earthquakes, we demonstrated the flexibility of the proposed method, which is readily adaptable for the detection of low-frequency earthquakes by retraining only a local model.

Seismic Wavefield Reconstruction based on Compressed Sensing using Data-Driven Reduced-Order Model

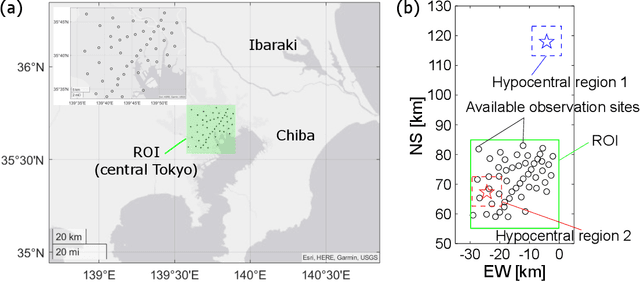
A seismic wavefield reconstruction framework based on compressed sensing using the data-driven reduced-order model (ROM) is proposed and its characteristics are investigated through numerical experiments. The data-driven ROM is generated from the dataset of the wavefield using the singular value decomposition. The spatially continuous seismic wavefield is reconstructed from the sparse and discrete observation and the data-driven ROM. The observation sites used for reconstruction are effectively selected by the sensor optimization method for linear inverse problems based on a greedy algorithm. The validity of the proposed method was confirmed by the reconstruction based on the noise-free observation. Since the ROM of the wavefield is used as prior information, the reconstruction error is reduced to an approximately lower error bound of the present framework, even though the number of sensors used for reconstruction is limited and randomly selected. In addition, the reconstruction error obtained by the proposed framework is much smaller than that obtained by the Gaussian process regression. For the numerical experiment with noise-contaminated observation, the reconstructed wavefield is degraded due to the observation noise, but the reconstruction error obtained by the present framework with all available observation sites is close to a lower error bound, even though the reconstructed wavefield using the Gaussian process regression is fully collapsed. Although the reconstruction error is larger than that obtained using all observation sites, the number of observation sites used for reconstruction can be reduced while minimizing the deterioration and scatter of the reconstructed data by combining it with the sensor optimization method.

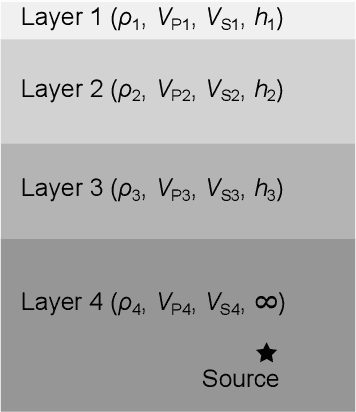
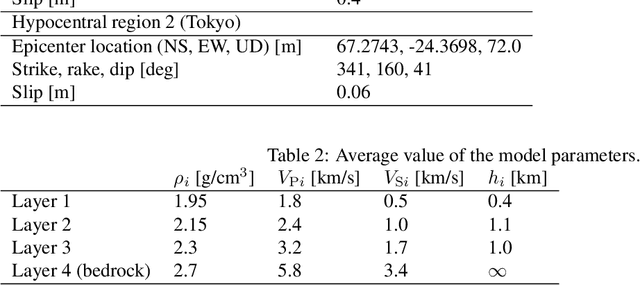
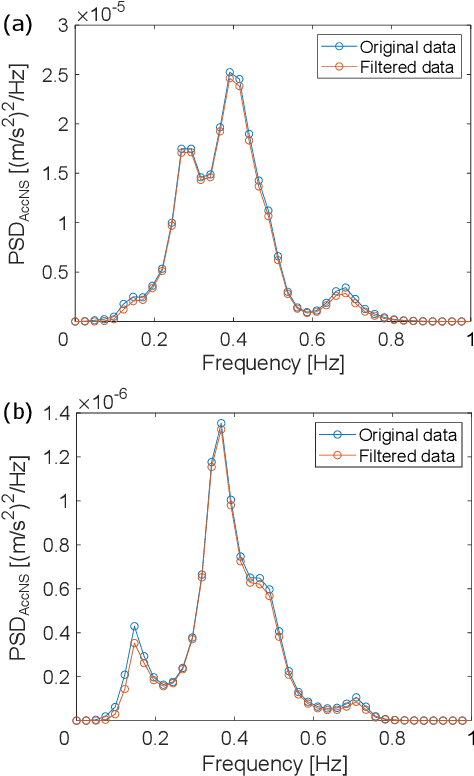
Observation Site Selection for Physical Model Parameter Estimation toward Process-Driven Seismic Wavefield Reconstruction

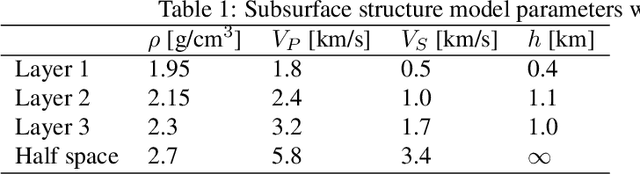
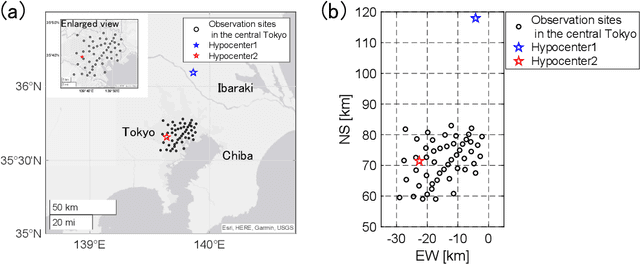
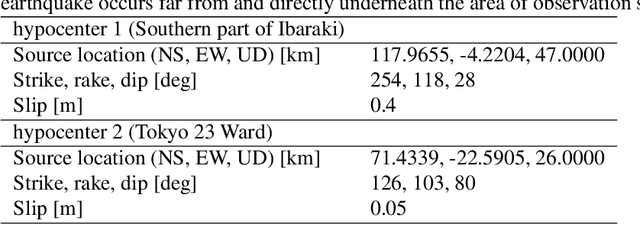
The seismic data not only acquired by seismometers but also acquired by vibrometers installed in buildings and infrastructure and accelerometers installed in smartphones will be certainly utilized for seismic research in the near future. Since it is impractical to utilize all the seismic big data in terms of the computational cost, methods which can select observation sites depending on the purpose are indispensable. We propose an observation site selection method for the accurate reconstruction of the seismic wavefield by process-driven approaches. The proposed method selects observation sites suitable for accurately estimating physical model parameters such as subsurface structures and source information to be input into a numerical simulation of the seismic wavefield. The seismic wavefield is reconstructed by the numerical simulation using the parameters estimated based on the observed signals at only observation sites selected by the proposed method. The observation site selection in the proposed method is based on the sensitivity of each observation site candidate to the physical model parameters; the matrix corresponding to the sensitivity is constructed by approximately calculating the derivatives based on the simulations, and then, observation sites are selected by evaluating the quantity of the sensitivity matrix based on the D-optimality criterion proposed in the optimal design of experiments. In the present study, physical knowledge on the sensitivity to the parameters such as seismic velocity, layer thickness, and hypocenter location was obtained by investigating the characteristics of the sensitivity matrix. Furthermore, the effectiveness of the proposed method was shown by verifying the accuracy of seismic wavefield reconstruction using the observation sites selected by the proposed method.

Multi-dimensional Graph Fourier Transform

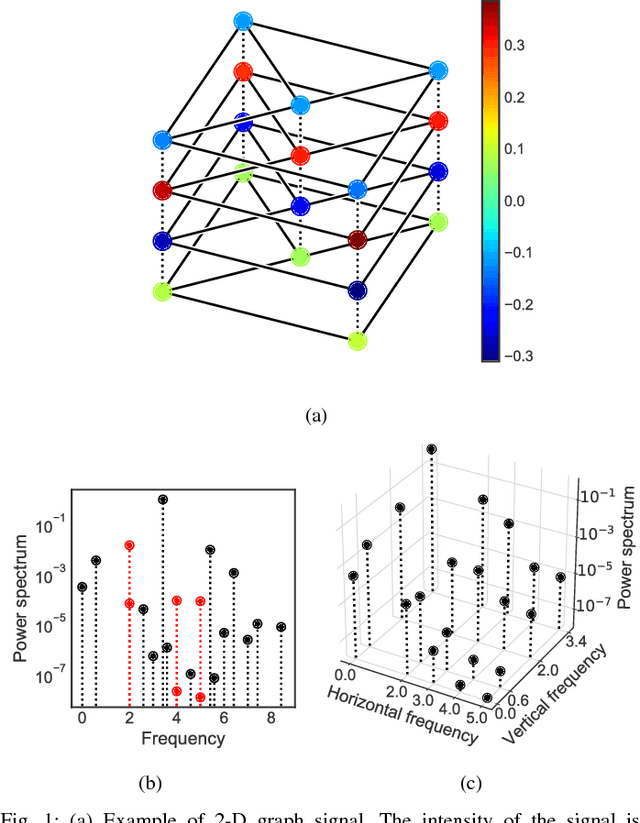
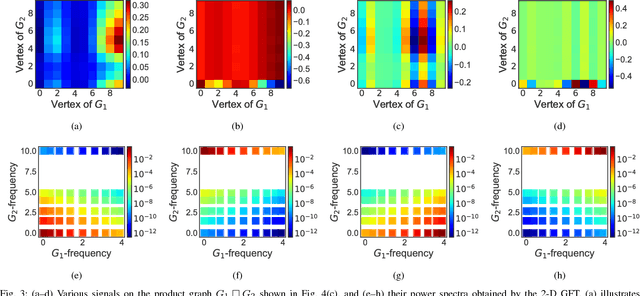
Many signals on Cartesian product graphs appear in the real world, such as digital images, sensor observation time series, and movie ratings on Netflix. These signals are "multi-dimensional" and have directional characteristics along each factor graph. However, the existing graph Fourier transform does not distinguish these directions, and assigns 1-D spectra to signals on product graphs. Further, these spectra are often multi-valued at some frequencies. Our main result is a multi-dimensional graph Fourier transform that solves such problems associated with the conventional GFT. Using algebraic properties of Cartesian products, the proposed transform rearranges 1-D spectra obtained by the conventional GFT into the multi-dimensional frequency domain, of which each dimension represents a directional frequency along each factor graph. Thus, the multi-dimensional graph Fourier transform enables directional frequency analysis, in addition to frequency analysis with the conventional GFT. Moreover, this rearrangement resolves the multi-valuedness of spectra in some cases. The multi-dimensional graph Fourier transform is a foundation of novel filterings and stationarities that utilize dimensional information of graph signals, which are also discussed in this study. The proposed methods are applicable to a wide variety of data that can be regarded as signals on Cartesian product graphs. This study also notes that multivariate graph signals can be regarded as 2-D univariate graph signals. This correspondence provides natural definitions of the multivariate graph Fourier transform and the multivariate stationarity based on their 2-D univariate versions.