Nondominated-Solution-based Multiobjective-Greedy Sensor Selection for Optimal Design of Experiments

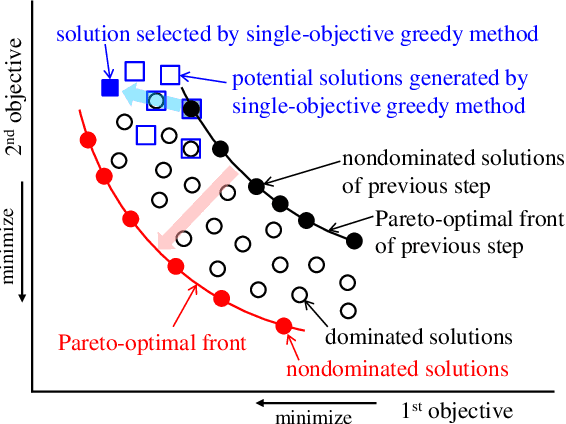
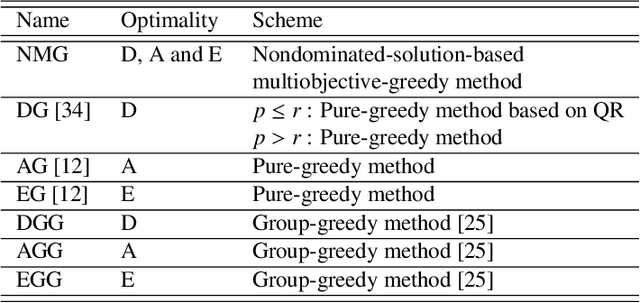
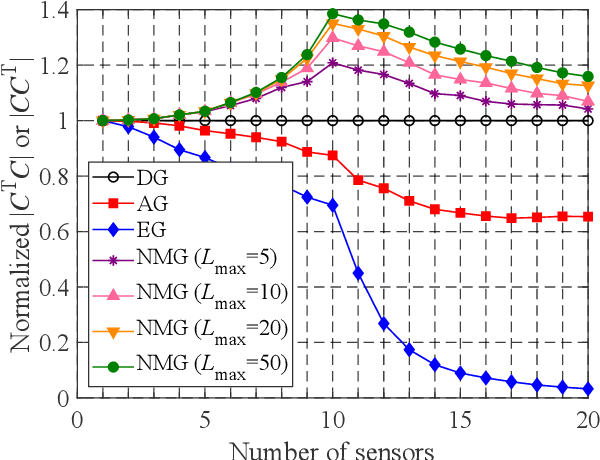
In this study, a nondominated-solution-based multiobjective-greedy sensor selection method for the optimal design of experiments is proposed and its performance is investigated. The proposed method simultaneously considers D-, A- and E-optimality and applies the idea of Pareto ranking to select the sensor set. With the proposed method, a new sensor is iteratively added to the nondominated solutions of sensor sets, and the multiobjective functions are evaluated for new sets of sensors based on increments in the relevant optimality index. The nondominated solutions are selected from the examined solutions, and the next sensor sets are then considered. With this procedure, the multiobjective optimization of sensor selection can be conducted with reasonable computational costs. The results show that the proposed method not only gives the Pareto-optimal front of the multiobjective optimization problem but also produces sets of sensors in terms of D-, A- and E-optimality, that are superior to the sets selected by pure-greedy methods that consider only a single objective function.