Understanding LLMs Requires More Than Statistical Generalization

The last decade has seen blossoming research in deep learning theory attempting to answer, "Why does deep learning generalize?" A powerful shift in perspective precipitated this progress: the study of overparametrized models in the interpolation regime. In this paper, we argue that another perspective shift is due, since some of the desirable qualities of LLMs are not a consequence of good statistical generalization and require a separate theoretical explanation. Our core argument relies on the observation that AR probabilistic models are inherently non-identifiable: models zero or near-zero KL divergence apart -- thus, equivalent test loss -- can exhibit markedly different behaviors. We support our position with mathematical examples and empirical observations, illustrating why non-identifiability has practical relevance through three case studies: (1) the non-identifiability of zero-shot rule extrapolation; (2) the approximate non-identifiability of in-context learning; and (3) the non-identifiability of fine-tunability. We review promising research directions focusing on LLM-relevant generalization measures, transferability, and inductive biases.

Estimating optimal PAC-Bayes bounds with Hamiltonian Monte Carlo

An important yet underexplored question in the PAC-Bayes literature is how much tightness we lose by restricting the posterior family to factorized Gaussian distributions when optimizing a PAC-Bayes bound. We investigate this issue by estimating data-independent PAC-Bayes bounds using the optimal posteriors, comparing them to bounds obtained using MFVI. Concretely, we (1) sample from the optimal Gibbs posterior using Hamiltonian Monte Carlo, (2) estimate its KL divergence from the prior with thermodynamic integration, and (3) propose three methods to obtain high-probability bounds under different assumptions. Our experiments on the MNIST dataset reveal significant tightness gaps, as much as 5-6\% in some cases.

Rethinking Sharpness-Aware Minimization as Variational Inference

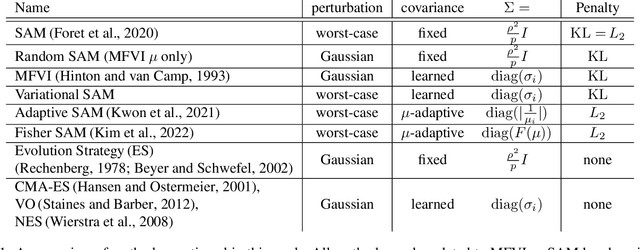
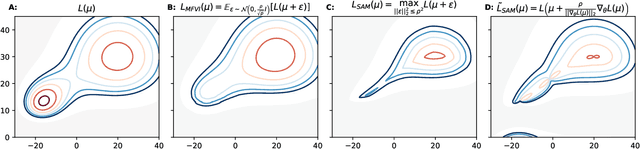
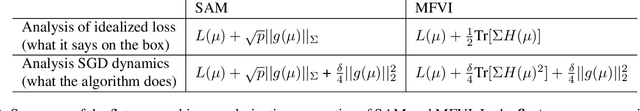
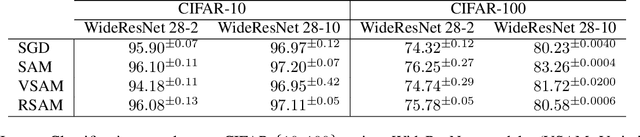
Sharpness-aware minimization (SAM) aims to improve the generalisation of gradient-based learning by seeking out flat minima. In this work, we establish connections between SAM and Mean-Field Variational Inference (MFVI) of neural network parameters. We show that both these methods have interpretations as optimizing notions of flatness, and when using the reparametrisation trick, they both boil down to calculating the gradient at a perturbed version of the current mean parameter. This thinking motivates our study of algorithms that combine or interpolate between SAM and MFVI. We evaluate the proposed variational algorithms on several benchmark datasets, and compare their performance to variants of SAM. Taking a broader perspective, our work suggests that SAM-like updates can be used as a drop-in replacement for the reparametrisation trick.