Understanding LLMs Requires More Than Statistical Generalization

The last decade has seen blossoming research in deep learning theory attempting to answer, "Why does deep learning generalize?" A powerful shift in perspective precipitated this progress: the study of overparametrized models in the interpolation regime. In this paper, we argue that another perspective shift is due, since some of the desirable qualities of LLMs are not a consequence of good statistical generalization and require a separate theoretical explanation. Our core argument relies on the observation that AR probabilistic models are inherently non-identifiable: models zero or near-zero KL divergence apart -- thus, equivalent test loss -- can exhibit markedly different behaviors. We support our position with mathematical examples and empirical observations, illustrating why non-identifiability has practical relevance through three case studies: (1) the non-identifiability of zero-shot rule extrapolation; (2) the approximate non-identifiability of in-context learning; and (3) the non-identifiability of fine-tunability. We review promising research directions focusing on LLM-relevant generalization measures, transferability, and inductive biases.

Expressiveness Remarks for Denoising Diffusion Models and Samplers

Denoising diffusion models are a class of generative models which have recently achieved state-of-the-art results across many domains. Gradual noise is added to the data using a diffusion process, which transforms the data distribution into a Gaussian. Samples from the generative model are then obtained by simulating an approximation of the time reversal of this diffusion initialized by Gaussian samples. Recent research has explored adapting diffusion models for sampling and inference tasks. In this paper, we leverage known connections to stochastic control akin to the F\"ollmer drift to extend established neural network approximation results for the F\"ollmer drift to denoising diffusion models and samplers.

Rethinking Sharpness-Aware Minimization as Variational Inference

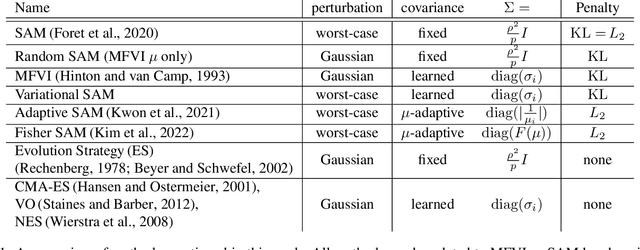
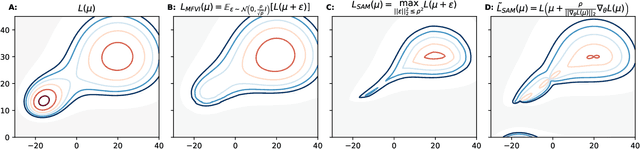
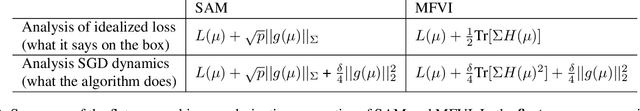
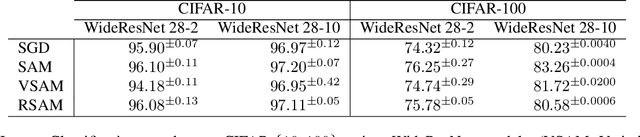
Sharpness-aware minimization (SAM) aims to improve the generalisation of gradient-based learning by seeking out flat minima. In this work, we establish connections between SAM and Mean-Field Variational Inference (MFVI) of neural network parameters. We show that both these methods have interpretations as optimizing notions of flatness, and when using the reparametrisation trick, they both boil down to calculating the gradient at a perturbed version of the current mean parameter. This thinking motivates our study of algorithms that combine or interpolate between SAM and MFVI. We evaluate the proposed variational algorithms on several benchmark datasets, and compare their performance to variants of SAM. Taking a broader perspective, our work suggests that SAM-like updates can be used as a drop-in replacement for the reparametrisation trick.

Depth Without the Magic: Inductive Bias of Natural Gradient Descent

In gradient descent, changing how we parametrize the model can lead to drastically different optimization trajectories, giving rise to a surprising range of meaningful inductive biases: identifying sparse classifiers or reconstructing low-rank matrices without explicit regularization. This implicit regularization has been hypothesised to be a contributing factor to good generalization in deep learning. However, natural gradient descent is approximately invariant to reparameterization, it always follows the same trajectory and finds the same optimum. The question naturally arises: What happens if we eliminate the role of parameterization, which solution will be found, what new properties occur? We characterize the behaviour of natural gradient flow in deep linear networks for separable classification under logistic loss and deep matrix factorization. Some of our findings extend to nonlinear neural networks with sufficient but finite over-parametrization. We demonstrate that there exist learning problems where natural gradient descent fails to generalize, while gradient descent with the right architecture performs well.