Sampling-Based Constrained Motion Planning with Products of Experts

We present a novel approach to enhance the performance of sampling-based Model Predictive Control (MPC) in constrained optimization by leveraging products of experts. Our methodology divides the main problem into two components: one focused on optimality and the other on feasibility. By combining the solutions from each component, represented as distributions, we apply products of experts to implement a project-then-sample strategy. In this strategy, the optimality distribution is projected into the feasible area, allowing for more efficient sampling. This approach contrasts with the traditional sample-then-project method, leading to more diverse exploration and reducing the accumulation of samples on the boundaries. We demonstrate an effective implementation of this principle using a tensor train-based distribution model, which is characterized by its non-parametric nature, ease of combination with other distributions at the task level, and straightforward sampling technique. We adapt existing tensor train models to suit this purpose and validate the efficacy of our approach through experiments in various tasks, including obstacle avoidance, non-prehensile manipulation, and tasks involving staying on manifolds. Our experimental results demonstrate that the proposed method consistently outperforms known baselines, providing strong empirical support for its effectiveness.

Robust Contact-rich Manipulation through Implicit Motor Adaptation

Contact-rich manipulation plays a vital role in daily human activities, yet uncertain physical parameters pose significant challenges for both model-based and model-free planning and control. A promising approach to address this challenge is to develop policies robust to a wide range of parameters. Domain adaptation and domain randomization are commonly used to achieve such policies but often compromise generalization to new instances or perform conservatively due to neglecting instance-specific information. \textit{Explicit motor adaptation} addresses these issues by estimating system parameters online and then retrieving the parameter-conditioned policy from a parameter-augmented base policy. However, it typically relies on precise system identification or additional high-quality policy retraining, presenting substantial challenges for contact-rich tasks with diverse physical parameters. In this work, we propose \textit{implicit motor adaptation}, which leverages tensor factorization as an implicit representation of the base policy. Given a roughly estimated parameter distribution, the parameter-conditioned policy can be efficiently derived by exploiting the separable structure of tensor cores from the base policy. This framework eliminates the need for precise system estimation and policy retraining while preserving optimal behavior and strong generalization. We provide a theoretical analysis validating this method, supported by numerical evaluations on three contact-rich manipulation primitives. Both simulation and real-world experiments demonstrate its ability to generate robust policies for diverse instances.

Robust Manipulation Primitive Learning via Domain Contraction

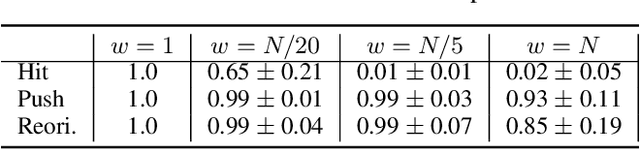
Contact-rich manipulation plays an important role in human daily activities, but uncertain parameters pose significant challenges for robots to achieve comparable performance through planning and control. To address this issue, domain adaptation and domain randomization have been proposed for robust policy learning. However, they either lose the generalization ability across diverse instances or perform conservatively due to neglecting instance-specific information. In this paper, we propose a bi-level approach to learn robust manipulation primitives, including parameter-augmented policy learning using multiple models, and parameter-conditioned policy retrieval through domain contraction. This approach unifies domain randomization and domain adaptation, providing optimal behaviors while keeping generalization ability. We validate the proposed method on three contact-rich manipulation primitives: hitting, pushing, and reorientation. The experimental results showcase the superior performance of our approach in generating robust policies for instances with diverse physical parameters.

Logic-Skill Programming: An Optimization-based Approach to Sequential Skill Planning

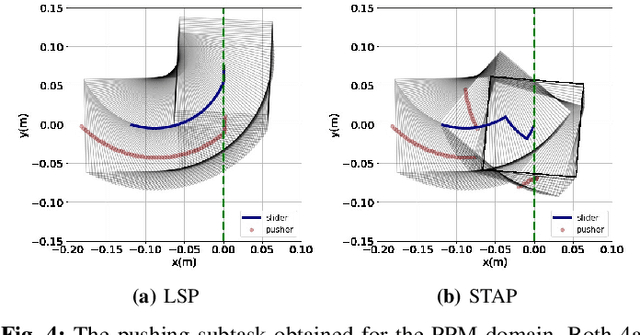
Recent advances in robot skill learning have unlocked the potential to construct task-agnostic skill libraries, facilitating the seamless sequencing of multiple simple manipulation primitives (aka. skills) to tackle significantly more complex tasks. Nevertheless, determining the optimal sequence for independently learned skills remains an open problem, particularly when the objective is given solely in terms of the final geometric configuration rather than a symbolic goal. To address this challenge, we propose Logic-Skill Programming (LSP), an optimization-based approach that sequences independently learned skills to solve long-horizon tasks. We formulate a first-order extension of a mathematical program to optimize the overall cumulative reward of all skills within a plan, abstracted by the sum of value functions. To solve such programs, we leverage the use of Tensor Train to construct the value function space, and rely on alternations between symbolic search and skill value optimization to find the appropriate skill skeleton and optimal subgoal sequence. Experimental results indicate that the obtained value functions provide a superior approximation of cumulative rewards compared to state-of-the-art Reinforcement Learning methods. Furthermore, we validate LSP in three manipulation domains, encompassing both prehensile and non-prehensile primitives. The results demonstrate its capability to identify the optimal solution over the full logic and geometric path. The real-robot experiments showcase the effectiveness of our approach to cope with contact uncertainty and external disturbances in the real world.

Tensor Train for Global Optimization Problems in Robotics

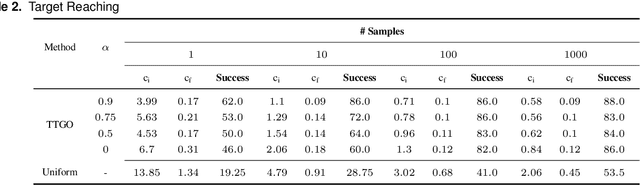
The convergence of many numerical optimization techniques is highly sensitive to the initial guess provided to the solver. We propose an approach based on tensor methods to initialize the existing optimization solvers close to global optima. The approach uses only the definition of the cost function and does not need access to any database of good solutions. We first transform the cost function, which is a function of task parameters and optimization variables, into a probability density function. Unlike existing approaches that set the task parameters as constant, we consider them as another set of random variables and approximate the joint probability distribution of the task parameters and the optimization variables using a surrogate probability model. For a given task, we then generate samples from the conditional distribution with respect to the given task parameter and use them as initialization for the optimization solver. As conditioning and sampling from an arbitrary density function are challenging, we use Tensor Train decomposition to obtain a surrogate probability model from which we can efficiently obtain the conditional model and the samples. The method can produce multiple solutions coming from different modes (when they exist) for a given task. We first evaluate the approach by applying it to various challenging benchmark functions for numerical optimization that are difficult to solve using gradient-based optimization solvers with a naive initialization, showing that the proposed method can produce samples close to the global optima and coming from multiple modes. We then demonstrate the generality of the framework and its relevance to robotics by applying the proposed method to inverse kinematics and motion planning problems with a 7-DoF manipulator.

Ergodic Exploration using Tensor Train: Applications in Insertion Tasks

By generating control policies that create natural search behaviors in autonomous systems, ergodic control provides a principled solution to address tasks that require exploration. A large class of ergodic control algorithms relies on spectral analysis, which suffers from the curse of dimensionality, both in storage and computation. This drawback has prohibited the application of ergodic control in robot manipulation since it often requires exploration in state space with more than 2 dimensions. Indeed, the original ergodic control formulation will typically not allow exploratory behaviors to be generated for a complete 6D end-effector pose. In this paper, we propose a solution for ergodic exploration based on the spectral analysis in multidimensional spaces using low-rank tensor approximation techniques. We rely on tensor train decomposition, a recent approach from multilinear algebra for low-rank approximation and efficient computation of multidimensional arrays. The proposed solution is efficient both computationally and storage-wise, hence making it suitable for its online implementation in robotic systems. The approach is applied to a peg-in-hole insertion task using a 7-axis Franka Emika Panda robot, where ergodic exploration allows the task to be achieved without requiring the use of force/torque sensors.