Steven Rosenberg
Understanding Natural Gradient in Sobolev Spaces
Feb 21, 2022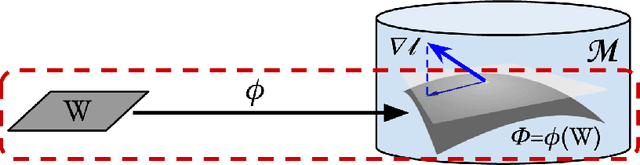
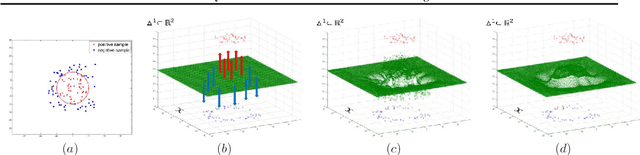
Abstract:While natural gradients have been widely studied from both theoretical and empirical perspectives, we argue that a fundamental theoretical issue regarding the existence of gradients in infinite dimensional function spaces remains underexplored. We therefore study the natural gradient induced by Sobolev metrics and develop several rigorous results. Our results also establish new connections between natural gradients and RKHS theory, and specifically to the Neural Tangent Kernel (NTK). We develop computational techniques for the efficient approximation of the proposed Sobolev Natural Gradient. Preliminary experimental results reveal the potential of this new natural gradient variant.
Occupant Plugload Management for Demand Response in Commercial Buildings: Field Experimentation and Statistical Characterization
Apr 22, 2020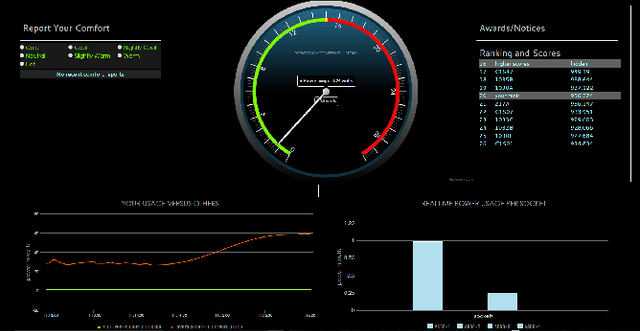
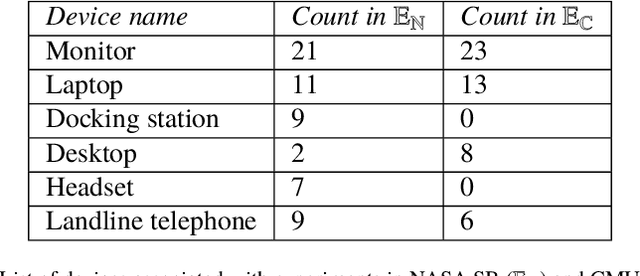
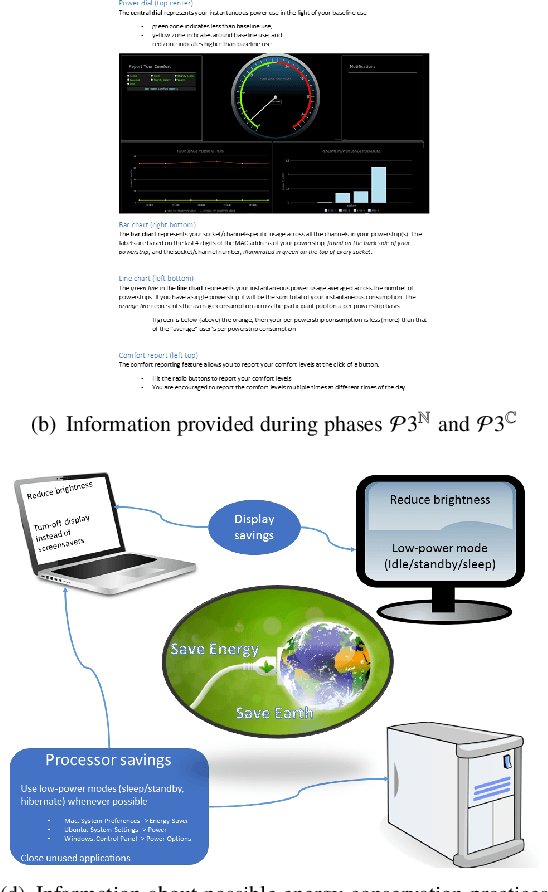
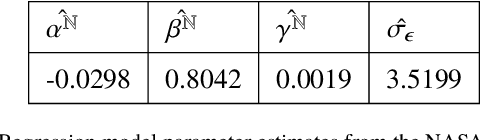
Abstract:Commercial buildings account for approximately 36% of US electricity consumption, of which nearly two-thirds is met by fossil fuels [1]. This sizeable consumption provided for by fossil fuels impacts the environment adversely. Reducing this impact requires improving energy efficiency by lowering energy consumption. Most existing studies focus on designing methods to regulate HVAC and Lighting consumption. However, few studies have focused on the regulation and control of occupant plugload consumption. To this end, we conducted multiple experiments to study changes in occupant plugload consumption due to monetary incentive and/or feedback. The experiments were performed in commercial and university buildings within the NASA Ames Research Center in Moffett Field, CA. Analysis of the data reveal significant plugload reduction can be achieved via feedback and/or incentive mechanisms. Autoregressive models are used to predict expected plugload savings in the presence of exogenous variables. The results of this study suggest that occupant-in-the-loop control architectures have the potential to yield considerable savings and reduce carbon emissions in the commercial building environment.
Class Probability Estimation via Differential Geometric Regularization
Feb 11, 2016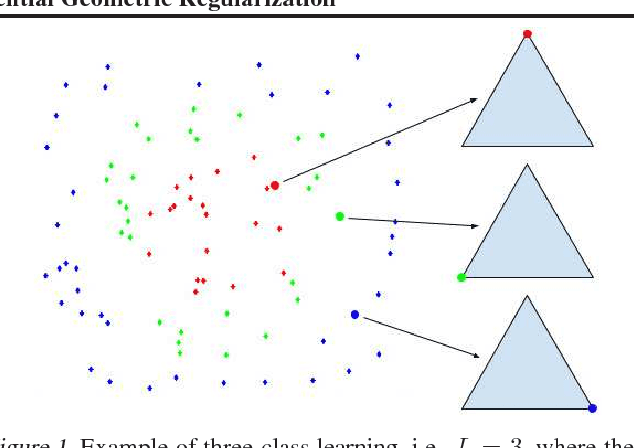
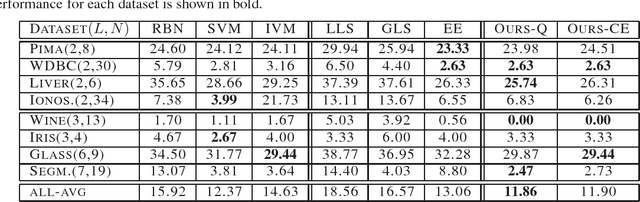

Abstract:We study the problem of supervised learning for both binary and multiclass classification from a unified geometric perspective. In particular, we propose a geometric regularization technique to find the submanifold corresponding to a robust estimator of the class probability $P(y|\pmb{x})$. The regularization term measures the volume of this submanifold, based on the intuition that overfitting produces rapid local oscillations and hence large volume of the estimator. This technique can be applied to regularize any classification function that satisfies two requirements: firstly, an estimator of the class probability can be obtained; secondly, first and second derivatives of the class probability estimator can be calculated. In experiments, we apply our regularization technique to standard loss functions for classification, our RBF-based implementation compares favorably to widely used regularization methods for both binary and multiclass classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge