Understanding Natural Gradient in Sobolev Spaces
Paper and Code
Feb 21, 2022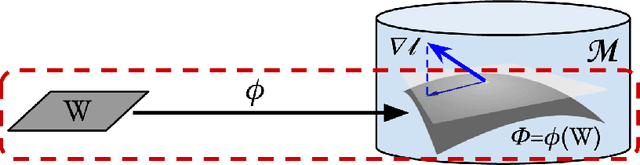
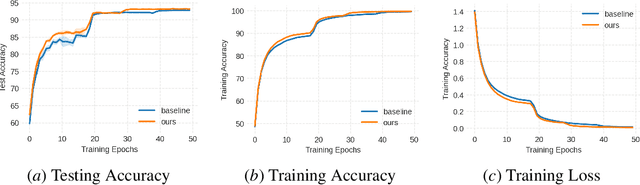
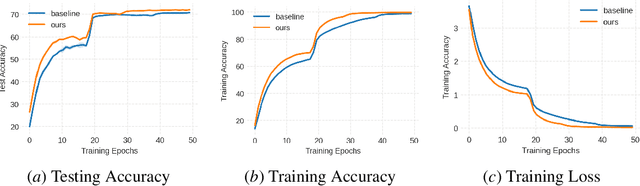
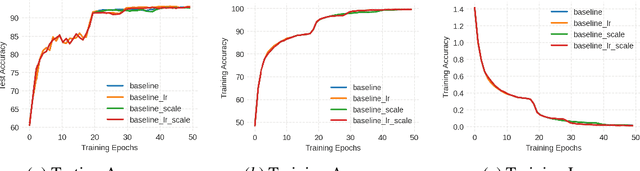
While natural gradients have been widely studied from both theoretical and empirical perspectives, we argue that a fundamental theoretical issue regarding the existence of gradients in infinite dimensional function spaces remains underexplored. We therefore study the natural gradient induced by Sobolev metrics and develop several rigorous results. Our results also establish new connections between natural gradients and RKHS theory, and specifically to the Neural Tangent Kernel (NTK). We develop computational techniques for the efficient approximation of the proposed Sobolev Natural Gradient. Preliminary experimental results reveal the potential of this new natural gradient variant.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge