Bayesian Classification and Feature Selection from Finite Data Sets

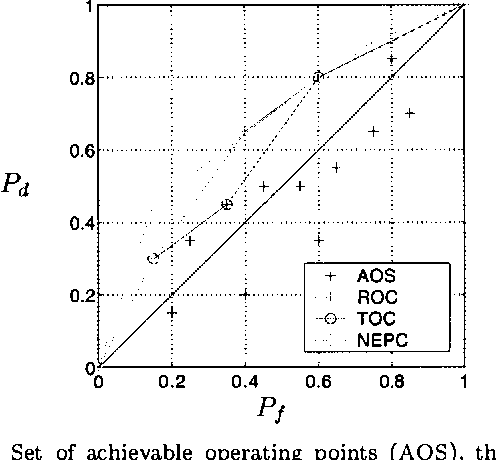
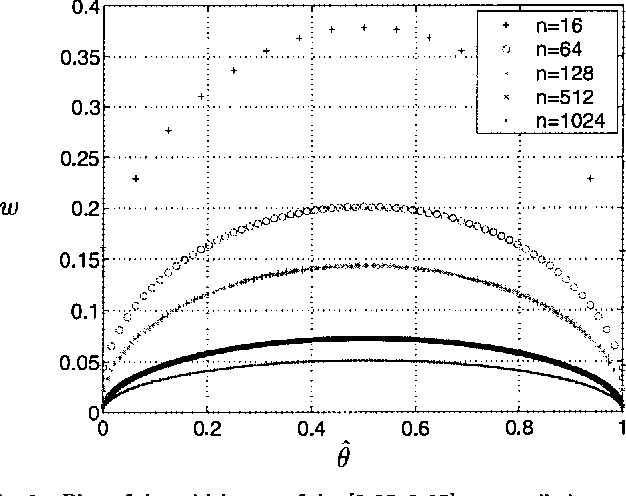
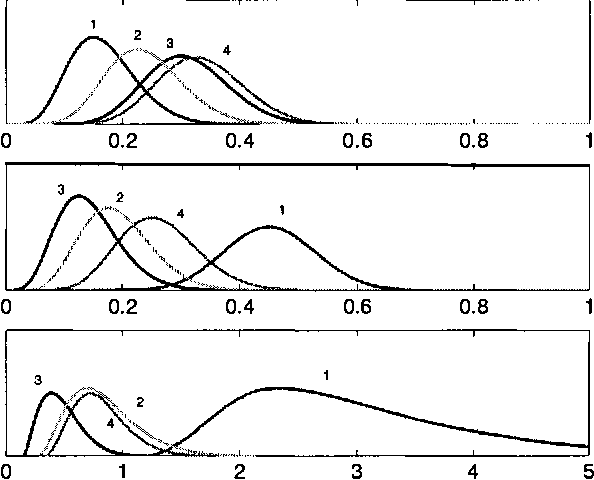
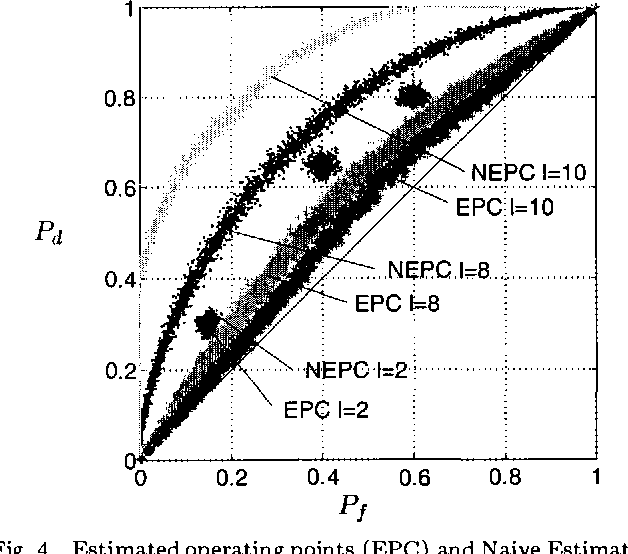
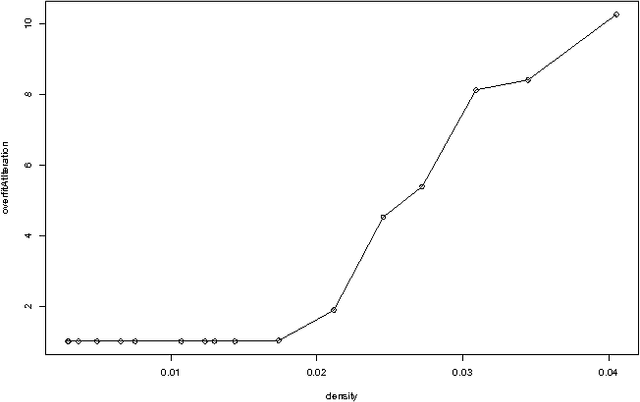
Feature selection aims to select the smallest subset of features for a specified level of performance. The optimal achievable classification performance on a feature subset is summarized by its Receiver Operating Curve (ROC). When infinite data is available, the Neyman- Pearson (NP) design procedure provides the most efficient way of obtaining this curve. In practice the design procedure is applied to density estimates from finite data sets. We perform a detailed statistical analysis of the resulting error propagation on finite alphabets. We show that the estimated performance curve (EPC) produced by the design procedure is arbitrarily accurate given sufficient data, independent of the size of the feature set. However, the underlying likelihood ranking procedure is highly sensitive to errors that reduces the probability that the EPC is in fact the ROC. In the worst case, guaranteeing that the EPC is equal to the ROC may require data sizes exponential in the size of the feature set. These results imply that in theory the NP design approach may only be valid for characterizing relatively small feature subsets, even when the performance of any given classifier can be estimated very accurately. We discuss the practical limitations for on-line methods that ensures that the NP procedure operates in a statistically valid region.

Probabilistic Models for Unified Collaborative and Content-Based Recommendation in Sparse-Data Environments

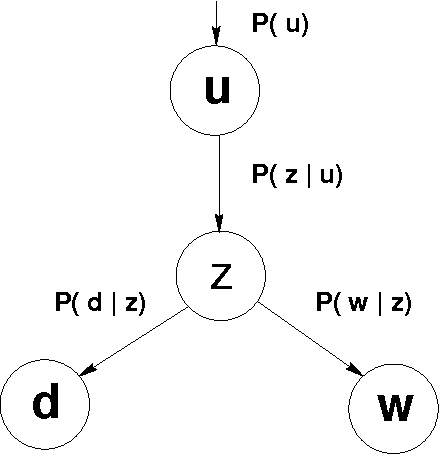
Recommender systems leverage product and community information to target products to consumers. Researchers have developed collaborative recommenders, content-based recommenders, and (largely ad-hoc) hybrid systems. We propose a unified probabilistic framework for merging collaborative and content-based recommendations. We extend Hofmann's [1999] aspect model to incorporate three-way co-occurrence data among users, items, and item content. The relative influence of collaboration data versus content data is not imposed as an exogenous parameter, but rather emerges naturally from the given data sources. Global probabilistic models coupled with standard Expectation Maximization (EM) learning algorithms tend to drastically overfit in sparse-data situations, as is typical in recommendation applications. We show that secondary content information can often be used to overcome sparsity. Experiments on data from the ResearchIndex library of Computer Science publications show that appropriate mixture models incorporating secondary data produce significantly better quality recommenders than k-nearest neighbors (k-NN). Global probabilistic models also allow more general inferences than local methods like k-NN.

1 Billion Pages = 1 Million Dollars? Mining the Web to Play "Who Wants to be a Millionaire?"

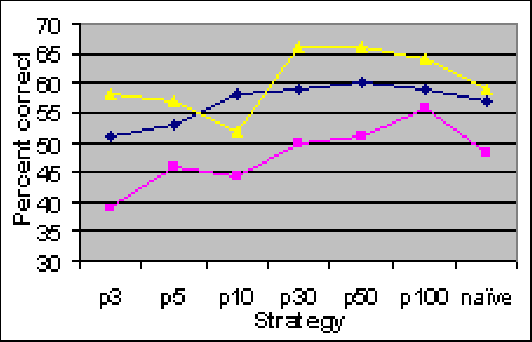
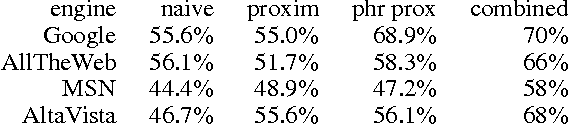
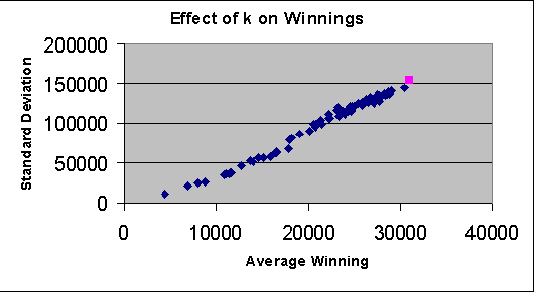
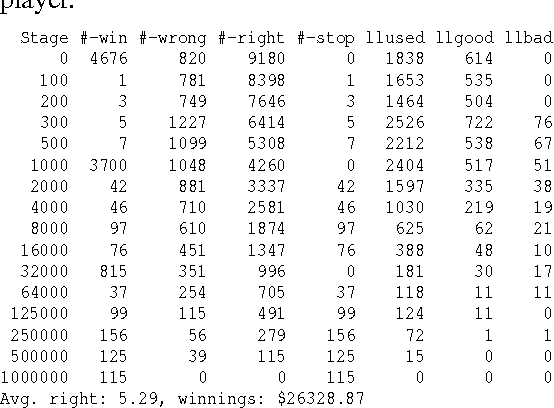
We exploit the redundancy and volume of information on the web to build a computerized player for the ABC TV game show 'Who Wants To Be A Millionaire?' The player consists of a question-answering module and a decision-making module. The question-answering module utilizes question transformation techniques, natural language parsing, multiple information retrieval algorithms, and multiple search engines; results are combined in the spirit of ensemble learning using an adaptive weighting scheme. Empirically, the system correctly answers about 75% of questions from the Millionaire CD-ROM, 3rd edition - general-interest trivia questions often about popular culture and common knowledge. The decision-making module chooses from allowable actions in the game in order to maximize expected risk-adjusted winnings, where the estimated probability of answering correctly is a function of past performance and confidence in in correctly answering the current question. When given a six question head start (i.e., when starting from the $2,000 level), we find that the system performs about as well on average as humans starting at the beginning. Our system demonstrates the potential of simple but well-chosen techniques for mining answers from unstructured information such as the web.