Dynamic Spectral Clustering with Provable Approximation Guarantee

This paper studies clustering algorithms for dynamically evolving graphs $\{G_t\}$, in which new edges (and potential new vertices) are added into a graph, and the underlying cluster structure of the graph can gradually change. The paper proves that, under some mild condition on the cluster-structure, the clusters of the final graph $G_T$ of $n_T$ vertices at time $T$ can be well approximated by a dynamic variant of the spectral clustering algorithm. The algorithm runs in amortised update time $O(1)$ and query time $o(n_T)$. Experimental studies on both synthetic and real-world datasets further confirm the practicality of our designed algorithm.

Nearly-Optimal Hierarchical Clustering for Well-Clustered Graphs

This paper presents two efficient hierarchical clustering (HC) algorithms with respect to Dasgupta's cost function. For any input graph $G$ with a clear cluster-structure, our designed algorithms run in nearly-linear time in the input size of $G$, and return an $O(1)$-approximate HC tree with respect to Dasgupta's cost function. We compare the performance of our algorithm against the previous state-of-the-art on synthetic and real-world datasets and show that our designed algorithm produces comparable or better HC trees with much lower running time.

On Episodes, Prototypical Networks, and Few-shot Learning

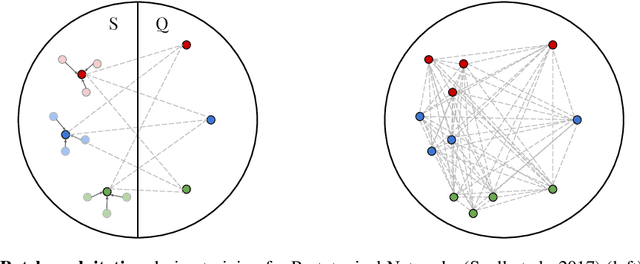
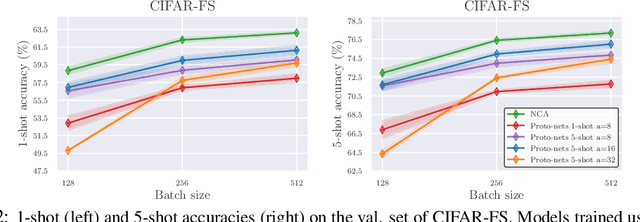
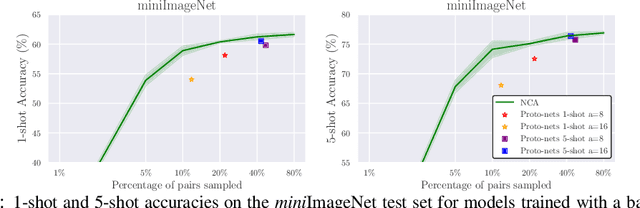
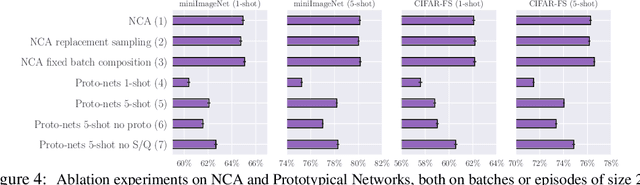
Episodic learning is a popular practice among researchers and practitioners interested in few-shot learning. It consists of organising training in a series of learning problems, each relying on small "support" and "query" sets to mimic the few-shot circumstances encountered during evaluation. In this paper, we investigate the usefulness of episodic learning in Prototypical Networks and Matching Networks, two of the most popular algorithms making use of this practice. Surprisingly, in our experiments we found that, for Prototypical and Matching Networks, it is detrimental to use the episodic learning strategy of separating training samples between support and query set, as it is a data-inefficient way to exploit training batches. These "non-episodic" variants, which are closely related to the classic Neighbourhood Component Analysis, reliably improve over their episodic counterparts in multiple datasets, achieving an accuracy that (in the case of Prototypical Networks) is competitive with the state-of-the-art, despite being extremely simple.

Higher-Order Spectral Clustering of Directed Graphs

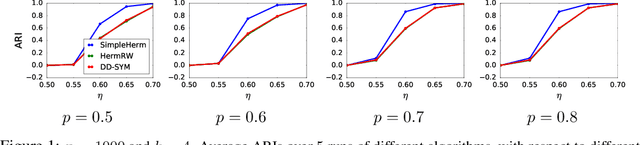
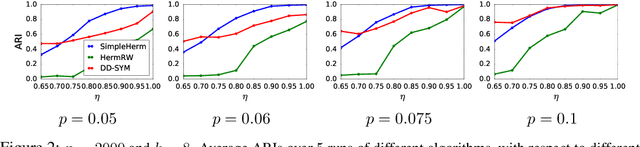
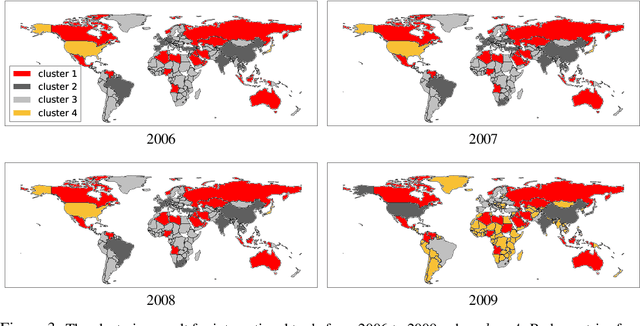
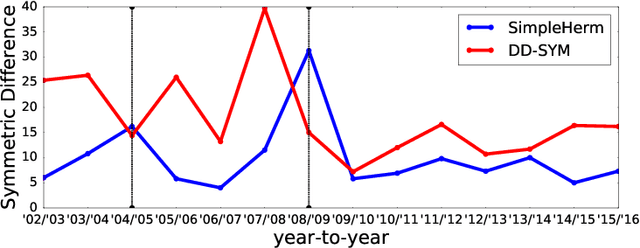
Clustering is an important topic in algorithms, and has a number of applications in machine learning, computer vision, statistics, and several other research disciplines. Traditional objectives of graph clustering are to find clusters with low conductance. Not only are these objectives just applicable for undirected graphs, they are also incapable to take the relationships between clusters into account, which could be crucial for many applications. To overcome these downsides, we study directed graphs (digraphs) whose clusters exhibit further "structural" information amongst each other. Based on the Hermitian matrix representation of digraphs, we present a nearly-linear time algorithm for digraph clustering, and further show that our proposed algorithm can be implemented in sublinear time under reasonable assumptions. The significance of our theoretical work is demonstrated by extensive experimental results on the UN Comtrade Dataset: the output clustering of our algorithm exhibits not only how the clusters (sets of countries) relate to each other with respect to their import and export records, but also how these clusters evolve over time, in accordance with known facts in international trade.