Peter Macgregor
Dynamic Similarity Graph Construction with Kernel Density Estimation
Jul 02, 2025Abstract:In the kernel density estimation (KDE) problem, we are given a set $X$ of data points in $\mathbb{R}^d$, a kernel function $k: \mathbb{R}^d \times \mathbb{R}^d \rightarrow \mathbb{R}$, and a query point $\mathbf{q} \in \mathbb{R}^d$, and the objective is to quickly output an estimate of $\sum_{\mathbf{x} \in X} k(\mathbf{q}, \mathbf{x})$. In this paper, we consider $\textsf{KDE}$ in the dynamic setting, and introduce a data structure that efficiently maintains the estimates for a set of query points as data points are added to $X$ over time. Based on this, we design a dynamic data structure that maintains a sparse approximation of the fully connected similarity graph on $X$, and develop a fast dynamic spectral clustering algorithm. We further evaluate the effectiveness of our algorithms on both synthetic and real-world datasets.
Dynamic DBSCAN with Euler Tour Sequences
Mar 11, 2025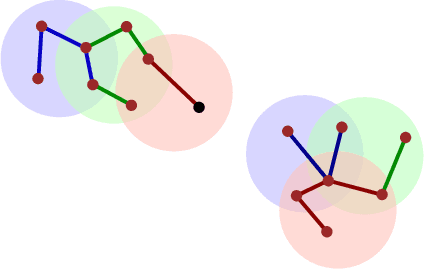
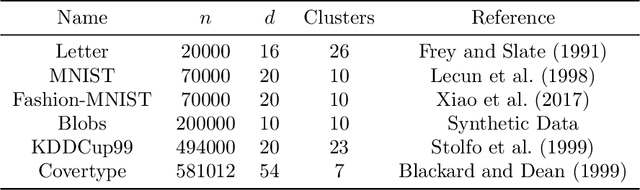
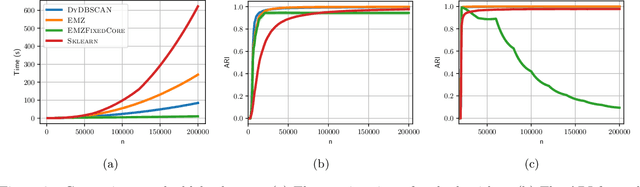
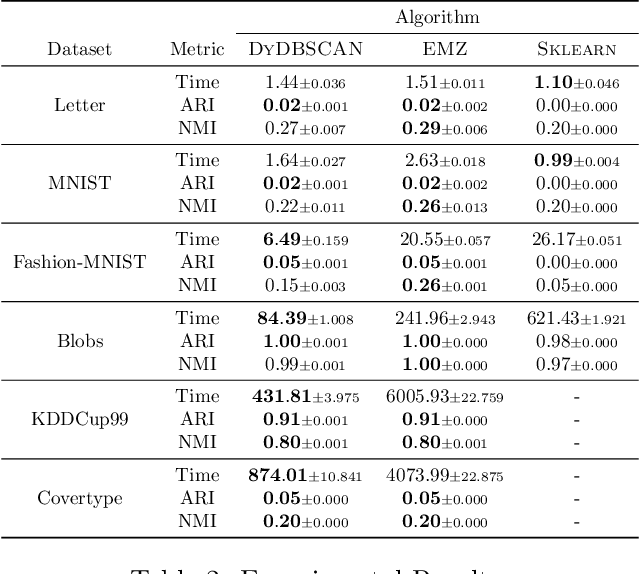
Abstract:We propose a fast and dynamic algorithm for Density-Based Spatial Clustering of Applications with Noise (DBSCAN) that efficiently supports online updates. Traditional DBSCAN algorithms, designed for batch processing, become computationally expensive when applied to dynamic datasets, particularly in large-scale applications where data continuously evolves. To address this challenge, our algorithm leverages the Euler Tour Trees data structure, enabling dynamic clustering updates without the need to reprocess the entire dataset. This approach preserves a near-optimal accuracy in density estimation, as achieved by the state-of-the-art static DBSCAN method (Esfandiari et al., 2021) Our method achieves an improved time complexity of $O(d \log^3(n) + \log^4(n))$ for every data point insertion and deletion, where $n$ and $d$ denote the total number of updates and the data dimension, respectively. Empirical studies also demonstrate significant speedups over conventional DBSCANs in real-time clustering of dynamic datasets, while maintaining comparable or superior clustering quality.
Coreset Spectral Clustering
Mar 10, 2025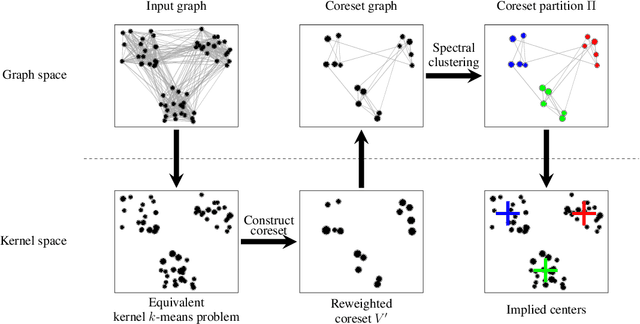
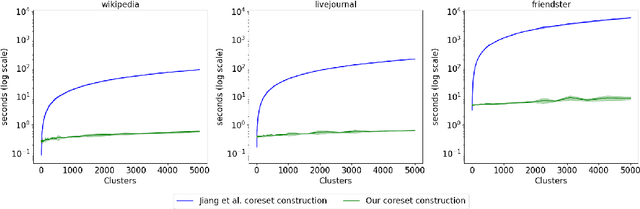
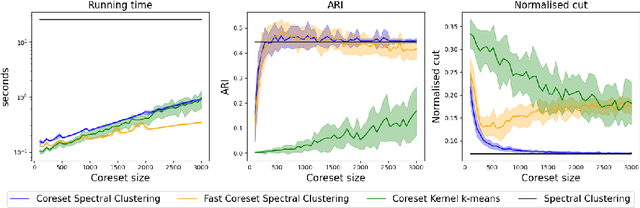
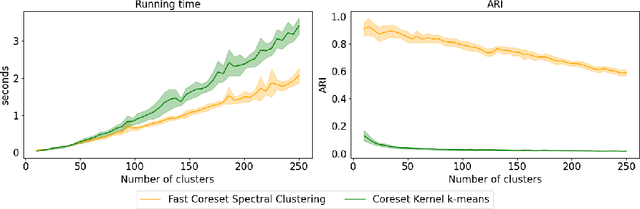
Abstract:Coresets have become an invaluable tool for solving $k$-means and kernel $k$-means clustering problems on large datasets with small numbers of clusters. On the other hand, spectral clustering works well on sparse graphs and has recently been extended to scale efficiently to large numbers of clusters. We exploit the connection between kernel $k$-means and the normalised cut problem to combine the benefits of both. Our main result is a coreset spectral clustering algorithm for graphs that clusters a coreset graph to infer a good labelling of the original graph. We prove that an $\alpha$-approximation for the normalised cut problem on the coreset graph is an $O(\alpha)$-approximation on the original. We also improve the running time of the state-of-the-art coreset algorithm for kernel $k$-means on sparse kernels, from $\tilde{O}(nk)$ to $\tilde{O}(n\cdot \min \{k, d_{avg}\})$, where $d_{avg}$ is the average number of non-zero entries in each row of the $n\times n$ kernel matrix. Our experiments confirm our coreset algorithm is asymptotically faster on large real-world graphs with many clusters, and show that our clustering algorithm overcomes the main challenge faced by coreset kernel $k$-means on sparse kernels which is getting stuck in local optima.
Fast Approximation of Similarity Graphs with Kernel Density Estimation
Oct 21, 2023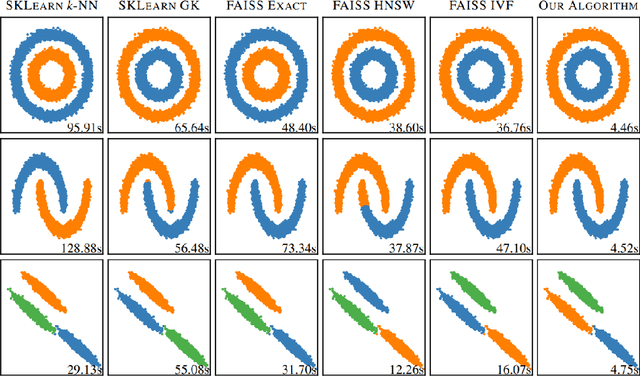
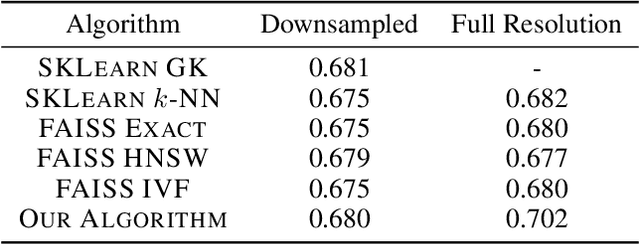
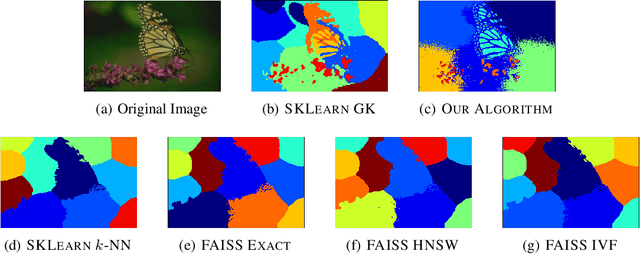
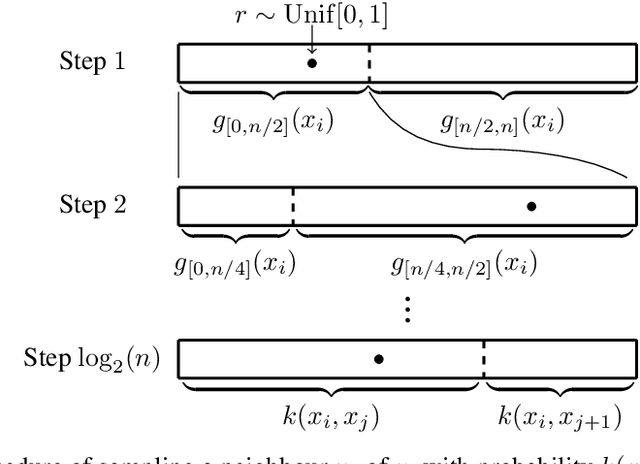
Abstract:Constructing a similarity graph from a set $X$ of data points in $\mathbb{R}^d$ is the first step of many modern clustering algorithms. However, typical constructions of a similarity graph have high time complexity, and a quadratic space dependency with respect to $|X|$. We address this limitation and present a new algorithmic framework that constructs a sparse approximation of the fully connected similarity graph while preserving its cluster structure. Our presented algorithm is based on the kernel density estimation problem, and is applicable for arbitrary kernel functions. We compare our designed algorithm with the well-known implementations from the scikit-learn library and the FAISS library, and find that our method significantly outperforms the implementation from both libraries on a variety of datasets.
Fast and Simple Spectral Clustering in Theory and Practice
Oct 17, 2023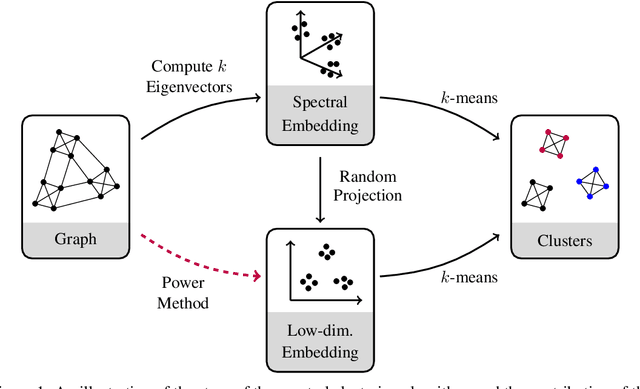
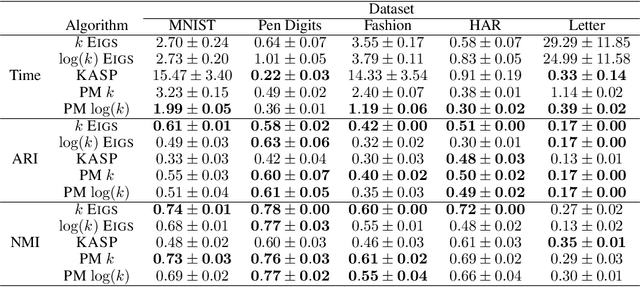
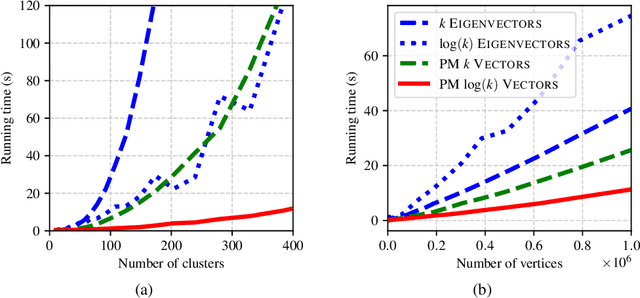
Abstract:Spectral clustering is a popular and effective algorithm designed to find $k$ clusters in a graph $G$. In the classical spectral clustering algorithm, the vertices of $G$ are embedded into $\mathbb{R}^k$ using $k$ eigenvectors of the graph Laplacian matrix. However, computing this embedding is computationally expensive and dominates the running time of the algorithm. In this paper, we present a simple spectral clustering algorithm based on a vertex embedding with $O(\log(k))$ vectors computed by the power method. The vertex embedding is computed in nearly-linear time with respect to the size of the graph, and the algorithm provably recovers the ground truth clusters under natural assumptions on the input graph. We evaluate the new algorithm on several synthetic and real-world datasets, finding that it is significantly faster than alternative clustering algorithms, while producing results with approximately the same clustering accuracy.
Spectral Toolkit of Algorithms for Graphs: Technical Report (1)
Apr 05, 2023Abstract:Spectral Toolkit of Algorithms for Graphs (STAG) is an open-source library for efficient spectral graph algorithms, and its development starts in September 2022. We have so far finished the component on local graph clustering, and this technical report presents a user's guide to STAG, showcase studies, and several technical considerations behind our development.
On Learning the Structure of Clusters in Graphs
Dec 29, 2022Abstract:Graph clustering is a fundamental problem in unsupervised learning, with numerous applications in computer science and in analysing real-world data. In many real-world applications, we find that the clusters have a significant high-level structure. This is often overlooked in the design and analysis of graph clustering algorithms which make strong simplifying assumptions about the structure of the graph. This thesis addresses the natural question of whether the structure of clusters can be learned efficiently and describes four new algorithmic results for learning such structure in graphs and hypergraphs. All of the presented theoretical results are extensively evaluated on both synthetic and real-word datasets of different domains, including image classification and segmentation, migration networks, co-authorship networks, and natural language processing. These experimental results demonstrate that the newly developed algorithms are practical, effective, and immediately applicable for learning the structure of clusters in real-world data.
A Tighter Analysis of Spectral Clustering, and Beyond
Aug 02, 2022

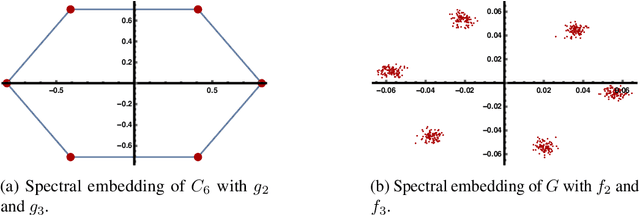
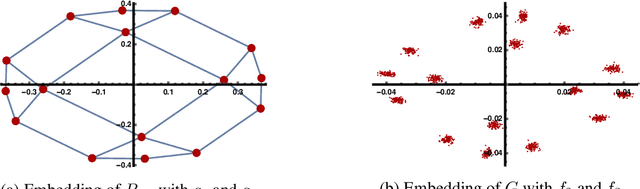
Abstract:This work studies the classical spectral clustering algorithm which embeds the vertices of some graph $G=(V_G, E_G)$ into $\mathbb{R}^k$ using $k$ eigenvectors of some matrix of $G$, and applies $k$-means to partition $V_G$ into $k$ clusters. Our first result is a tighter analysis on the performance of spectral clustering, and explains why it works under some much weaker condition than the ones studied in the literature. For the second result, we show that, by applying fewer than $k$ eigenvectors to construct the embedding, spectral clustering is able to produce better output for many practical instances; this result is the first of its kind in spectral clustering. Besides its conceptual and theoretical significance, the practical impact of our work is demonstrated by the empirical analysis on both synthetic and real-world datasets, in which spectral clustering produces comparable or better results with fewer than $k$ eigenvectors.
Finding Bipartite Components in Hypergraphs
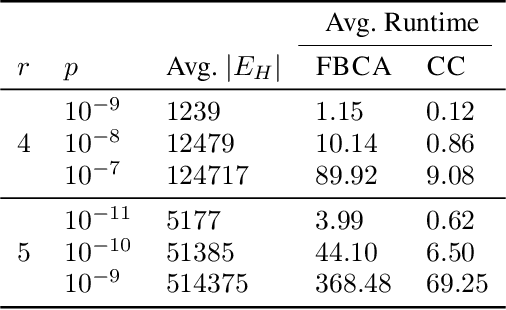
May 05, 2022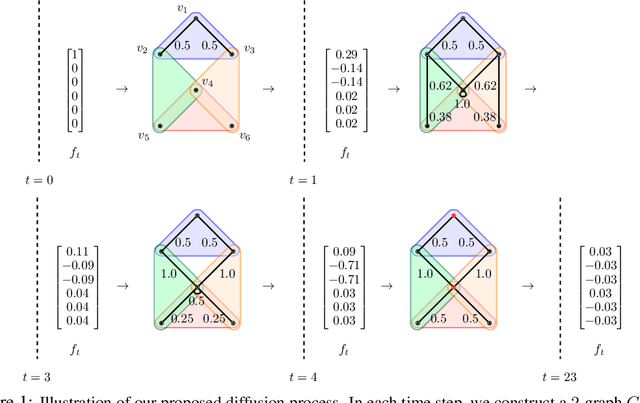
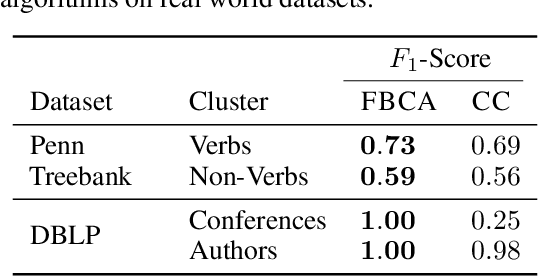
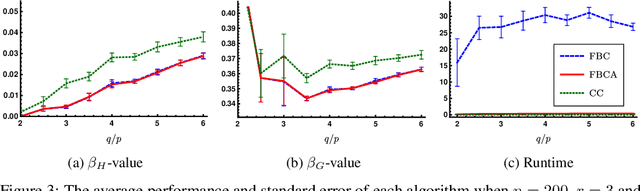
Abstract:Hypergraphs are important objects to model ternary or higher-order relations of objects, and have a number of applications in analysing many complex datasets occurring in practice. In this work we study a new heat diffusion process in hypergraphs, and employ this process to design a polynomial-time algorithm that approximately finds bipartite components in a hypergraph. We theoretically prove the performance of our proposed algorithm, and compare it against the previous state-of-the-art through extensive experimental analysis on both synthetic and real-world datasets. We find that our new algorithm consistently and significantly outperforms the previous state-of-the-art across a wide range of hypergraphs.
Local Algorithms for Finding Densely Connected Clusters
Jun 09, 2021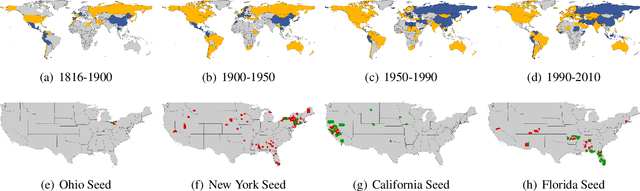
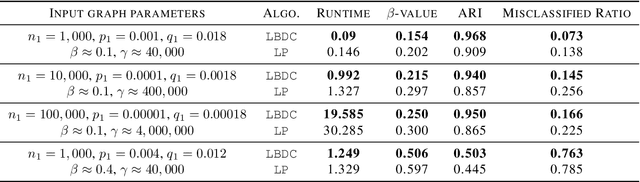
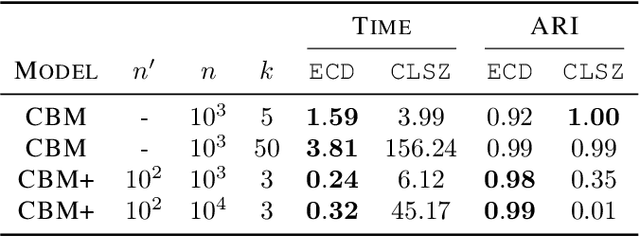
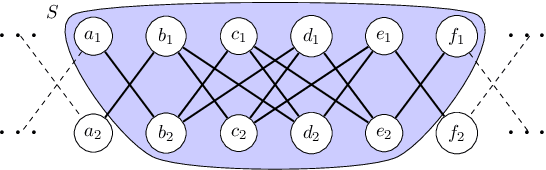
Abstract:Local graph clustering is an important algorithmic technique for analysing massive graphs, and has been widely applied in many research fields of data science. While the objective of most (local) graph clustering algorithms is to find a vertex set of low conductance, there has been a sequence of recent studies that highlight the importance of the inter-connection between clusters when analysing real-world datasets. Following this line of research, in this work we study local algorithms for finding a pair of vertex sets defined with respect to their inter-connection and their relationship with the rest of the graph. The key to our analysis is a new reduction technique that relates the structure of multiple sets to a single vertex set in the reduced graph. Among many potential applications, we show that our algorithms successfully recover densely connected clusters in the Interstate Disputes Dataset and the US Migration Dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge