Coreset Spectral Clustering

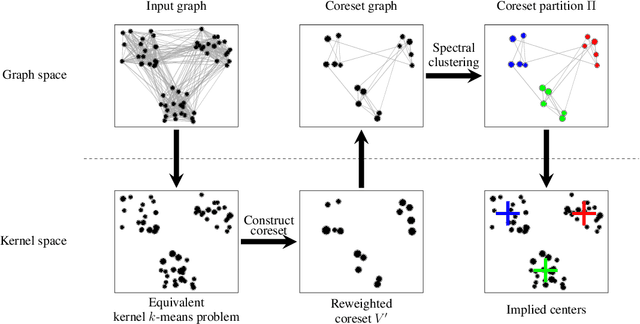
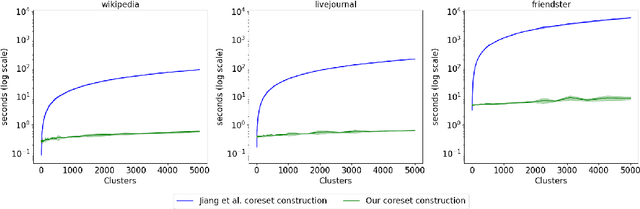
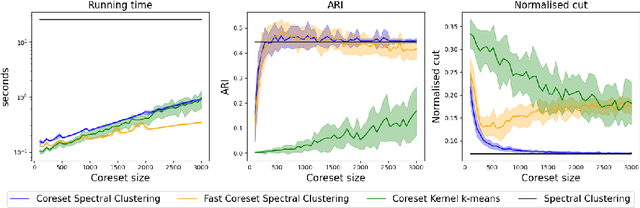
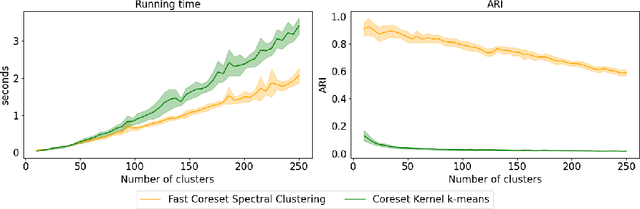
Coresets have become an invaluable tool for solving $k$-means and kernel $k$-means clustering problems on large datasets with small numbers of clusters. On the other hand, spectral clustering works well on sparse graphs and has recently been extended to scale efficiently to large numbers of clusters. We exploit the connection between kernel $k$-means and the normalised cut problem to combine the benefits of both. Our main result is a coreset spectral clustering algorithm for graphs that clusters a coreset graph to infer a good labelling of the original graph. We prove that an $\alpha$-approximation for the normalised cut problem on the coreset graph is an $O(\alpha)$-approximation on the original. We also improve the running time of the state-of-the-art coreset algorithm for kernel $k$-means on sparse kernels, from $\tilde{O}(nk)$ to $\tilde{O}(n\cdot \min \{k, d_{avg}\})$, where $d_{avg}$ is the average number of non-zero entries in each row of the $n\times n$ kernel matrix. Our experiments confirm our coreset algorithm is asymptotically faster on large real-world graphs with many clusters, and show that our clustering algorithm overcomes the main challenge faced by coreset kernel $k$-means on sparse kernels which is getting stuck in local optima.

Mini-Batch Kernel $k$-means

We present the first mini-batch kernel $k$-means algorithm, offering an order of magnitude improvement in running time compared to the full batch algorithm. A single iteration of our algorithm takes $\widetilde{O}(kb^2)$ time, significantly faster than the $O(n^2)$ time required by the full batch kernel $k$-means, where $n$ is the dataset size and $b$ is the batch size. Extensive experiments demonstrate that our algorithm consistently achieves a 10-100x speedup with minimal loss in quality, addressing the slow runtime that has limited kernel $k$-means adoption in practice. We further complement these results with a theoretical analysis under an early stopping condition, proving that with a batch size of $\widetilde{\Omega}(\max \{\gamma^{4}, \gamma^{2}\} \cdot \epsilon^{-2})$, the algorithm terminates in $O(\gamma^2/\epsilon)$ iterations with high probability, where $\gamma$ bounds the norm of points in feature space and $\epsilon$ is a termination threshold. Our analysis holds for any reasonable center initialization, and when using $k$-means++ initialization, the algorithm achieves an approximation ratio of $O(\log k)$ in expectation. For normalized kernels, such as Gaussian or Laplacian it holds that $\gamma=1$. Taking $\epsilon = O(1)$ and $b=\Theta(\log n)$, the algorithm terminates in $O(1)$ iterations, with each iteration running in $\widetilde{O}(k)$ time.

Exfiltration of personal information from ChatGPT via prompt injection

We report that ChatGPT 4 and 4o are susceptible to a prompt injection attack that allows an attacker to query users' personal data. It is applicable without the use of any 3rd party tools and all users are currently affected. This vulnerability is exacerbated by the recent introduction of ChatGPT's memory feature, which allows an attacker to command ChatGPT to monitor the user for the desired personal data.

Mini-batch Submodular Maximization

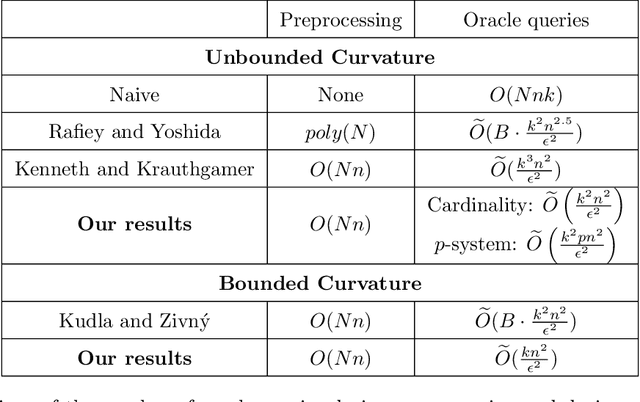
We present the first mini-batch algorithm for maximizing a non-negative monotone decomposable submodular function, $F=\sum_{i=1}^N f^i$, under a set of constraints. We improve over the sparsifier based approach both in theory and in practice. We experimentally observe that our algorithm generates solutions that are far superior to those generated by the sparsifier based approach.

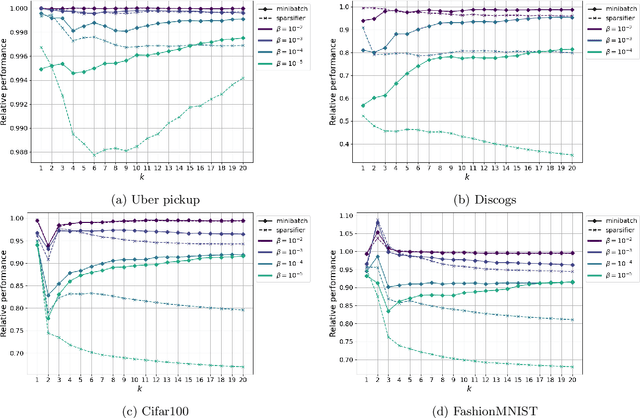
Mini-batch $k$-means terminates within $O$ iterations

We answer the question: "Does local progress (on batches) imply global progress (on the entire dataset) for mini-batch $k$-means?". Specifically, we consider mini-batch $k$-means which terminates only when the improvement in the quality of the clustering on the sampled batch is below some threshold. Although at first glance it appears that this algorithm might execute forever, we answer the above question in the affirmative and show that if the batch is of size $\tilde{\Omega}((d/\epsilon)^2)$, it must terminate within $O(d/\epsilon)$ iterations with high probability, where $d$ is the dimension of the input, and $\epsilon$ is a threshold parameter for termination. This is true regardless of how the centers are initialized. When the algorithm is initialized with the $k$-means++ initialization scheme, it achieves an approximation ratio of $O(\log k)$ (the same as the full-batch version). Finally, we show the applicability of our results to the mini-batch $k$-means algorithm implemented in the scikit-learn (sklearn) python library.

SGD Through the Lens of Kolmogorov Complexity

We prove that stochastic gradient descent (SGD) finds a solution that achieves $(1-\epsilon)$ classification accuracy on the entire dataset. We do so under two main assumptions: (1. Local progress) There is consistent improvement of the model accuracy over batches. (2. Models compute simple functions) The function computed by the model is simple (has low Kolmogorov complexity). Intuitively, the above means that \emph{local progress} of SGD implies \emph{global progress}. Assumption 2 trivially holds for underparameterized models, hence, our work gives the first convergence guarantee for general, \emph{underparameterized models}. Furthermore, this is the first result which is completely \emph{model agnostic} - we don't require the model to have any specific architecture or activation function, it may not even be a neural network. Our analysis makes use of the entropy compression method, which was first introduced by Moser and Tardos in the context of the Lov\'asz local lemma.