Higher-Order Spectral Clustering of Directed Graphs
Paper and Code
Nov 10, 2020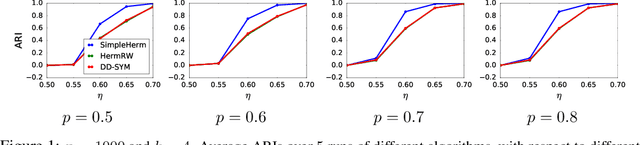
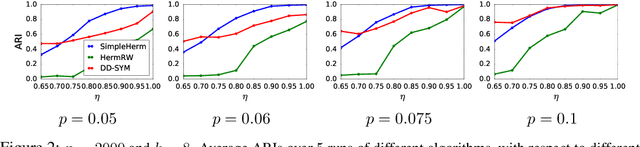
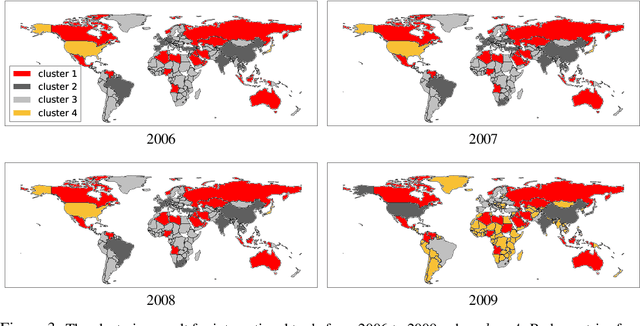
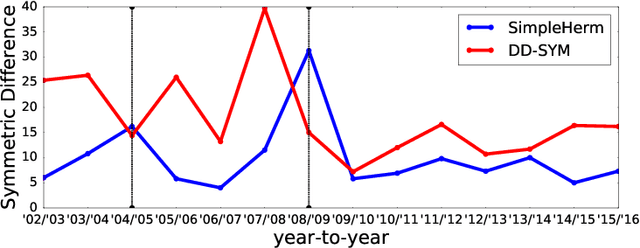
Clustering is an important topic in algorithms, and has a number of applications in machine learning, computer vision, statistics, and several other research disciplines. Traditional objectives of graph clustering are to find clusters with low conductance. Not only are these objectives just applicable for undirected graphs, they are also incapable to take the relationships between clusters into account, which could be crucial for many applications. To overcome these downsides, we study directed graphs (digraphs) whose clusters exhibit further "structural" information amongst each other. Based on the Hermitian matrix representation of digraphs, we present a nearly-linear time algorithm for digraph clustering, and further show that our proposed algorithm can be implemented in sublinear time under reasonable assumptions. The significance of our theoretical work is demonstrated by extensive experimental results on the UN Comtrade Dataset: the output clustering of our algorithm exhibits not only how the clusters (sets of countries) relate to each other with respect to their import and export records, but also how these clusters evolve over time, in accordance with known facts in international trade.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge