Constraints on the design of neuromorphic circuits set by the properties of neural population codes

In the brain, information is encoded, transmitted and used to inform behaviour at the level of timing of action potentials distributed over population of neurons. To implement neural-like systems in silico, to emulate neural function, and to interface successfully with the brain, neuromorphic circuits need to encode information in a way compatible to that used by populations of neuron in the brain. To facilitate the cross-talk between neuromorphic engineering and neuroscience, in this Review we first critically examine and summarize emerging recent findings about how population of neurons encode and transmit information. We examine the effects on encoding and readout of information for different features of neural population activity, namely the sparseness of neural representations, the heterogeneity of neural properties, the correlations among neurons, and the time scales (from short to long) at which neurons encode information and maintain it consistently over time. Finally, we critically elaborate on how these facts constrain the design of information coding in neuromorphic circuits. We focus primarily on the implications for designing neuromorphic circuits that communicate with the brain, as in this case it is essential that artificial and biological neurons use compatible neural codes. However, we also discuss implications for the design of neuromorphic systems for implementation or emulation of neural computation.

Causal learning with sufficient statistics: an information bottleneck approach

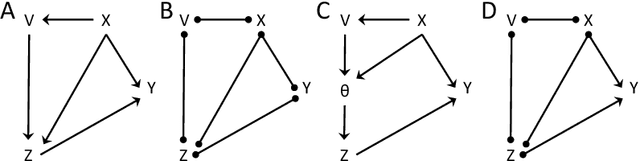
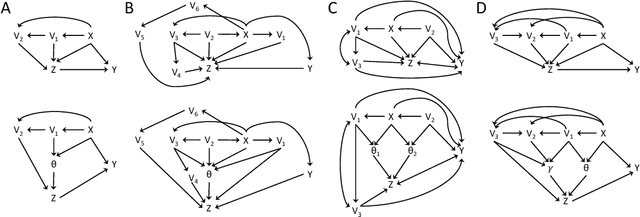
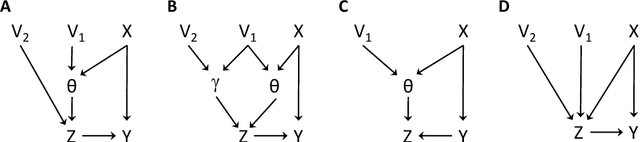
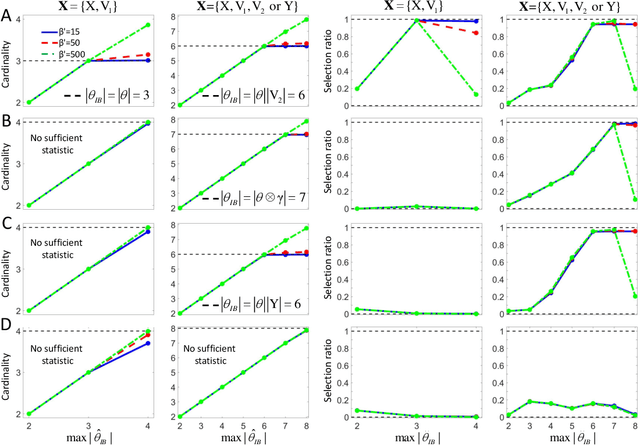
The inference of causal relationships using observational data from partially observed multivariate systems with hidden variables is a fundamental question in many scientific domains. Methods extracting causal information from conditional independencies between variables of a system are common tools for this purpose, but are limited in the lack of independencies. To surmount this limitation, we capitalize on the fact that the laws governing the generative mechanisms of a system often result in substructures embodied in the generative functional equation of a variable, which act as sufficient statistics for the influence that other variables have on it. These functional sufficient statistics constitute intermediate hidden variables providing new conditional independencies to be tested. We propose to use the Information Bottleneck method, a technique commonly applied for dimensionality reduction, to find underlying sufficient sets of statistics. Using these statistics we formulate new additional rules of causal orientation that provide causal information not obtainable from standard structure learning algorithms, which exploit only conditional independencies between observable variables. We validate the use of sufficient statistics for structure learning both with simulated systems built to contain specific sufficient statistics and with benchmark data from regulatory rules previously and independently proposed to model biological signal transduction networks.

Conditionally-additive-noise Models for Structure Learning

Constraint-based structure learning algorithms infer the causal structure of multivariate systems from observational data by determining an equivalent class of causal structures compatible with the conditional independencies in the data. Methods based on additive-noise (AN) models have been proposed to further discriminate between causal structures that are equivalent in terms of conditional independencies. These methods rely on a particular form of the generative functional equations, with an additive noise structure, which allows inferring the directionality of causation by testing the independence between the residuals of a nonlinear regression and the predictors (nrr-independencies). Full causal structure identifiability has been proven for systems that contain only additive-noise equations and have no hidden variables. We extend the AN framework in several ways. We introduce alternative regression-free tests of independence based on conditional variances (cv-independencies). We consider conditionally-additive-noise (CAN) models, in which the equations may have the AN form only after conditioning. We exploit asymmetries in nrr-independencies or cv-independencies resulting from the CAN form to derive a criterion that infers the causal relation between a pair of variables in a multivariate system without any assumption about the form of the equations or the presence of hidden variables.

Synthesizing realistic neural population activity patterns using Generative Adversarial Networks

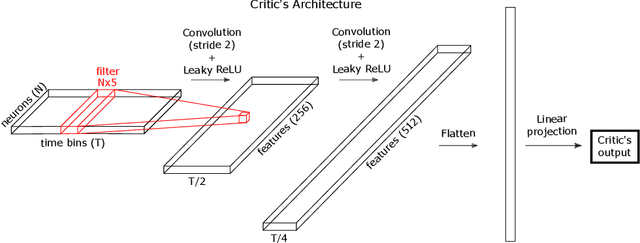
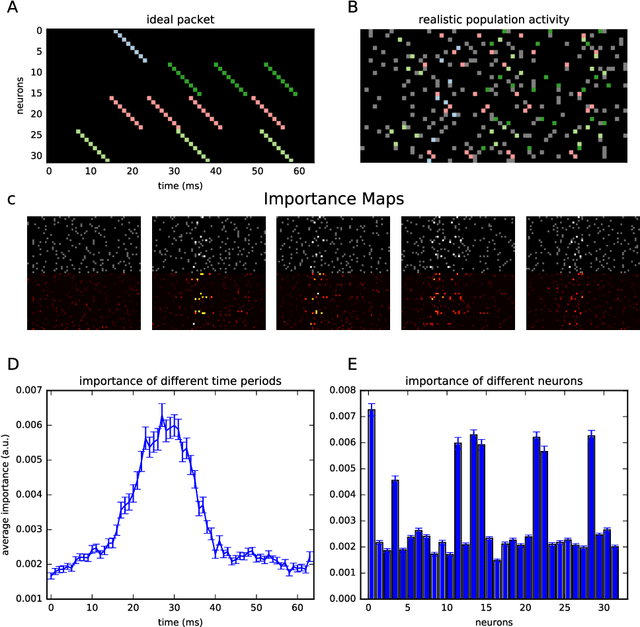
The ability to synthesize realistic patterns of neural activity is crucial for studying neural information processing. Here we used the Generative Adversarial Networks (GANs) framework to simulate the concerted activity of a population of neurons. We adapted the Wasserstein-GAN variant to facilitate the generation of unconstrained neural population activity patterns while still benefiting from parameter sharing in the temporal domain. We demonstrate that our proposed GAN, which we termed Spike-GAN, generates spike trains that match accurately the first- and second-order statistics of datasets of tens of neurons and also approximates well their higher-order statistics. We applied Spike-GAN to a real dataset recorded from salamander retina and showed that it performs as well as state-of-the-art approaches based on the maximum entropy and the dichotomized Gaussian frameworks. Importantly, Spike-GAN does not require to specify a priori the statistics to be matched by the model, and so constitutes a more flexible method than these alternative approaches. Finally, we show how to exploit a trained Spike-GAN to construct 'importance maps' to detect the most relevant statistical structures present in a spike train. Spike-GAN provides a powerful, easy-to-use technique for generating realistic spiking neural activity and for describing the most relevant features of the large-scale neural population recordings studied in modern systems neuroscience.

The identity of information: how deterministic dependencies constrain information synergy and redundancy

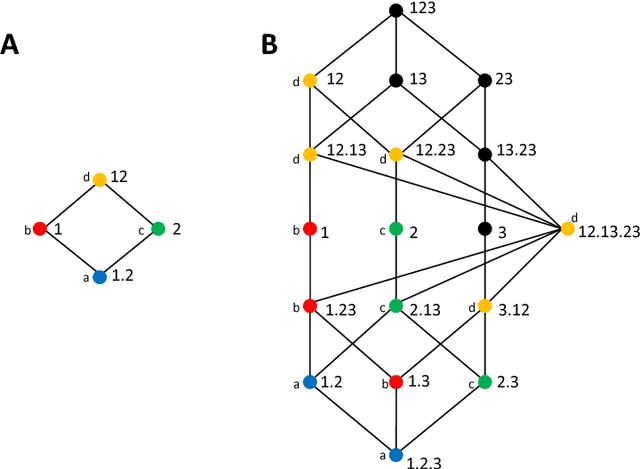
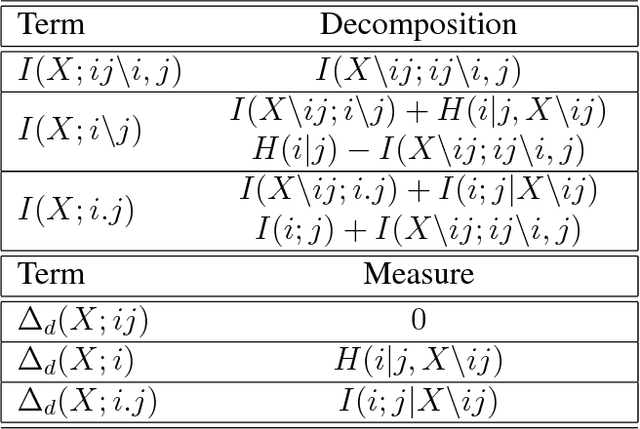
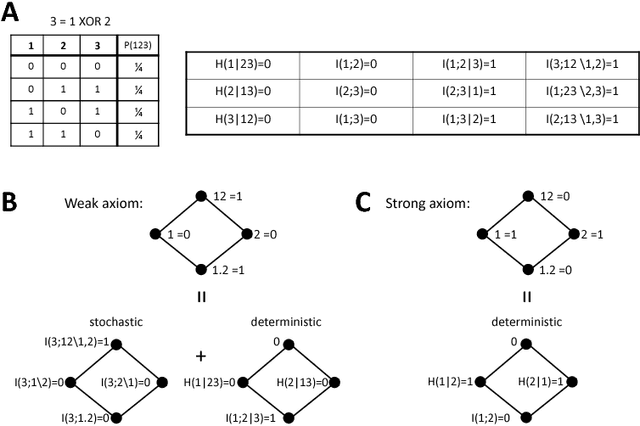
Understanding how different information sources together transmit information is crucial in many domains. For example, understanding the neural code requires characterizing how different neurons contribute unique, redundant, or synergistic pieces of information about sensory or behavioral variables. Williams and Beer (2010) proposed a partial information decomposition (PID) which separates the mutual information that a set of sources contains about a set of targets into nonnegative terms interpretable as these pieces. Quantifying redundancy requires assigning an identity to different information pieces, to assess when information is common across sources. Harder et al. (2013) proposed an identity axiom stating that there cannot be redundancy between two independent sources about a copy of themselves. However, Bertschinger et al. (2012) showed that with a deterministically related sources-target copy this axiom is incompatible with ensuring PID nonnegativity. Here we study systematically the effect of deterministic target-sources dependencies. We introduce two synergy stochasticity axioms that generalize the identity axiom, and we derive general expressions separating stochastic and deterministic PID components. Our analysis identifies how negative terms can originate from deterministic dependencies and shows how different assumptions on information identity, implicit in the stochasticity and identity axioms, determine the PID structure. The implications for studying neural coding are discussed.

Invariant components of synergy, redundancy, and unique information among three variables

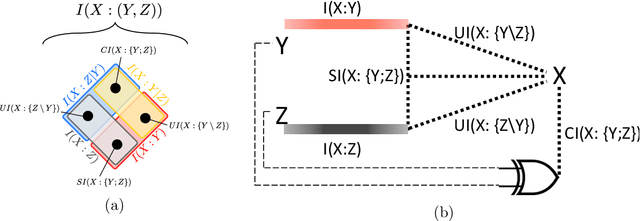
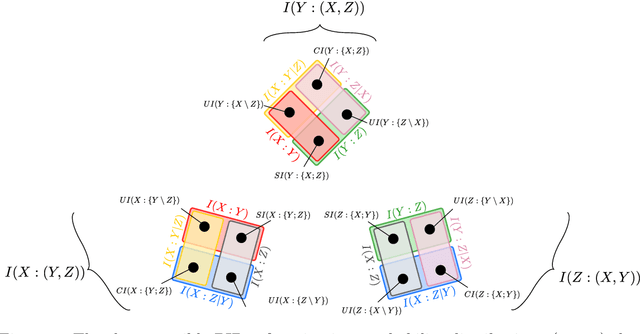
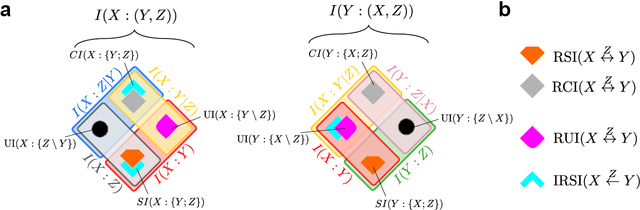
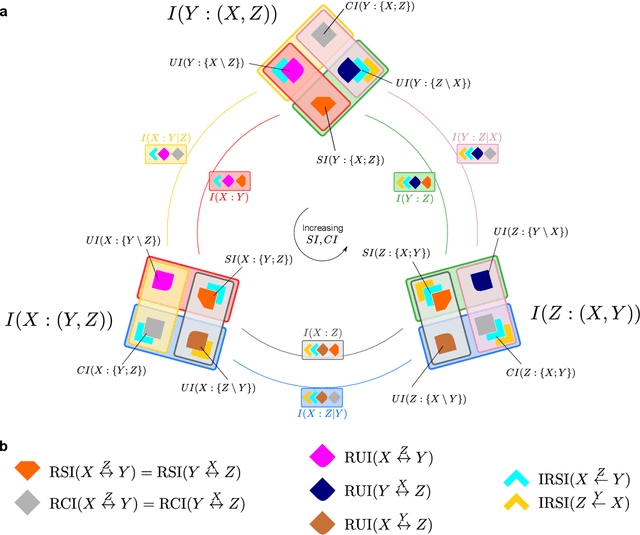
In a system of three stochastic variables, the Partial Information Decomposition (PID) of Williams and Beer dissects the information that two variables (sources) carry about a third variable (target) into nonnegative information atoms that describe redundant, unique, and synergistic modes of dependencies among the variables. However, the classification of the three variables into two sources and one target limits the dependency modes that can be quantitatively resolved, and does not naturally suit all systems. Here, we extend the PID to describe trivariate modes of dependencies in full generality, without introducing additional decomposition axioms or making assumptions about the target/source nature of the variables. By comparing different PID lattices of the same system, we unveil a finer PID structure made of seven nonnegative information subatoms that are invariant to different target/source classifications and that are sufficient to construct any PID lattice. This finer structure naturally splits redundant information into two nonnegative components: the source redundancy, which arises from the pairwise correlations between the source variables, and the non-source redundancy, which does not, and relates to the synergistic information the sources carry about the target. The invariant structure is also sufficient to construct the system's entropy, hence it characterizes completely all the interdependencies in the system.