The identity of information: how deterministic dependencies constrain information synergy and redundancy

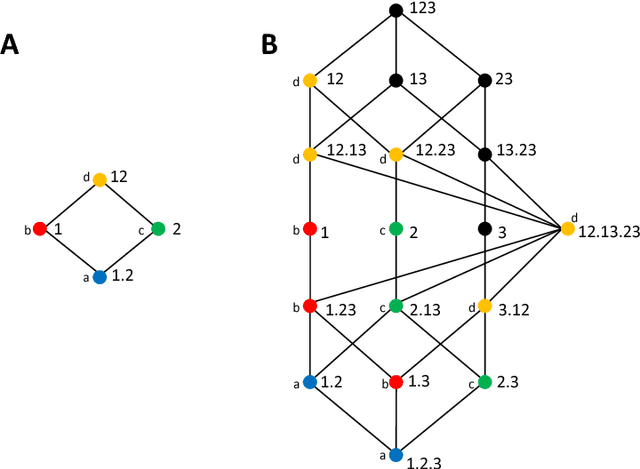
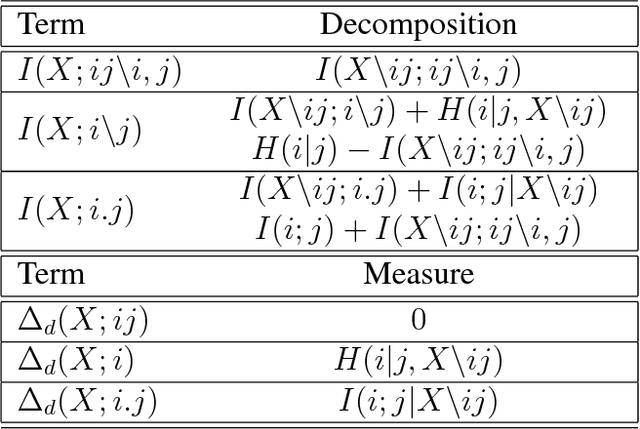
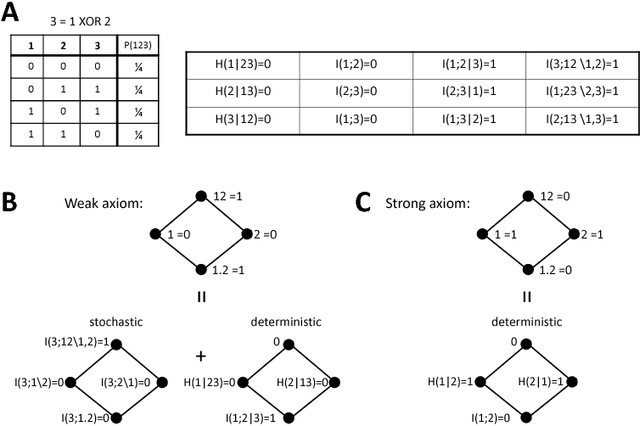
Understanding how different information sources together transmit information is crucial in many domains. For example, understanding the neural code requires characterizing how different neurons contribute unique, redundant, or synergistic pieces of information about sensory or behavioral variables. Williams and Beer (2010) proposed a partial information decomposition (PID) which separates the mutual information that a set of sources contains about a set of targets into nonnegative terms interpretable as these pieces. Quantifying redundancy requires assigning an identity to different information pieces, to assess when information is common across sources. Harder et al. (2013) proposed an identity axiom stating that there cannot be redundancy between two independent sources about a copy of themselves. However, Bertschinger et al. (2012) showed that with a deterministically related sources-target copy this axiom is incompatible with ensuring PID nonnegativity. Here we study systematically the effect of deterministic target-sources dependencies. We introduce two synergy stochasticity axioms that generalize the identity axiom, and we derive general expressions separating stochastic and deterministic PID components. Our analysis identifies how negative terms can originate from deterministic dependencies and shows how different assumptions on information identity, implicit in the stochasticity and identity axioms, determine the PID structure. The implications for studying neural coding are discussed.