PolyWorld: Polygonal Building Extraction with Graph Neural Networks in Satellite Images

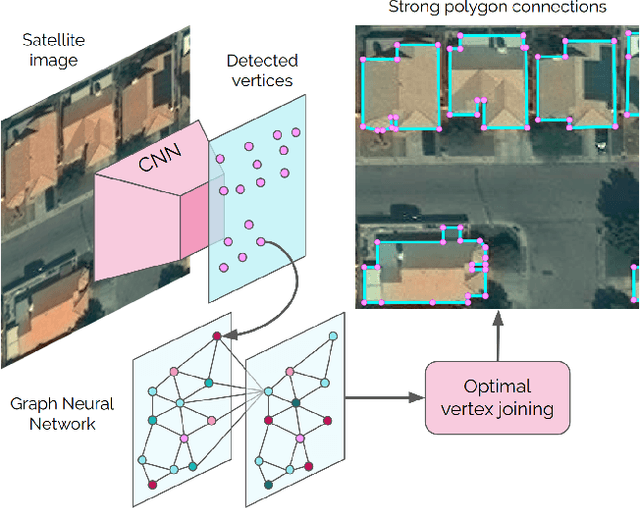
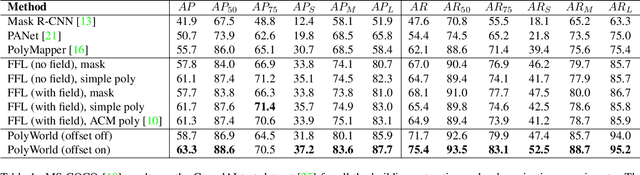
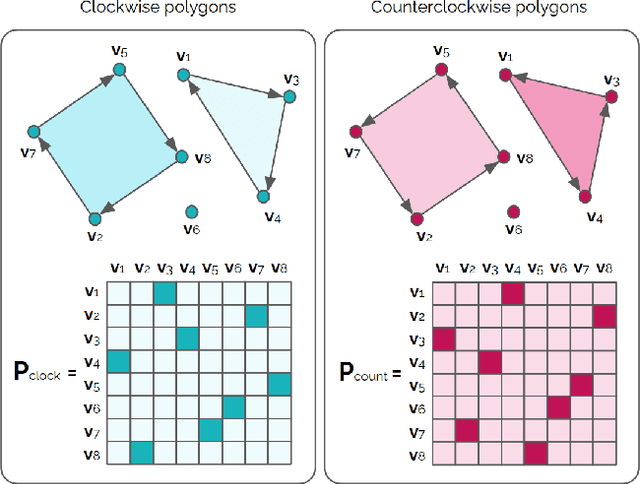
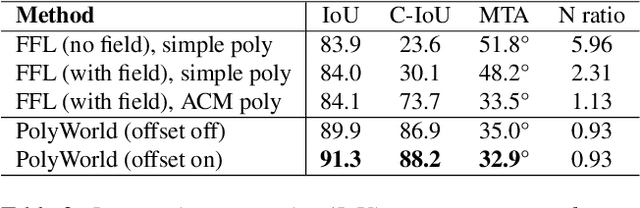
Most state-of-the-art instance segmentation methods produce binary segmentation masks, however, geographic and cartographic applications typically require precise vector polygons of extracted objects instead of rasterized output. This paper introduces PolyWorld, a neural network that directly extracts building vertices from an image and connects them correctly to create precise polygons. The model predicts the connection strength between each pair of vertices using a graph neural network and estimates the assignments by solving a differentiable optimal transport problem. Moreover, the vertex positions are optimized by minimizing a combined segmentation and polygonal angle difference loss. PolyWorld significantly outperforms the state-of-the-art in building polygonization and achieves not only notable quantitative results, but also produces visually pleasing building polygons. Code and trained weights will be soon available on github.

A dynamic connectome supports the emergence of stable computational function of neural circuits through reward-based learning

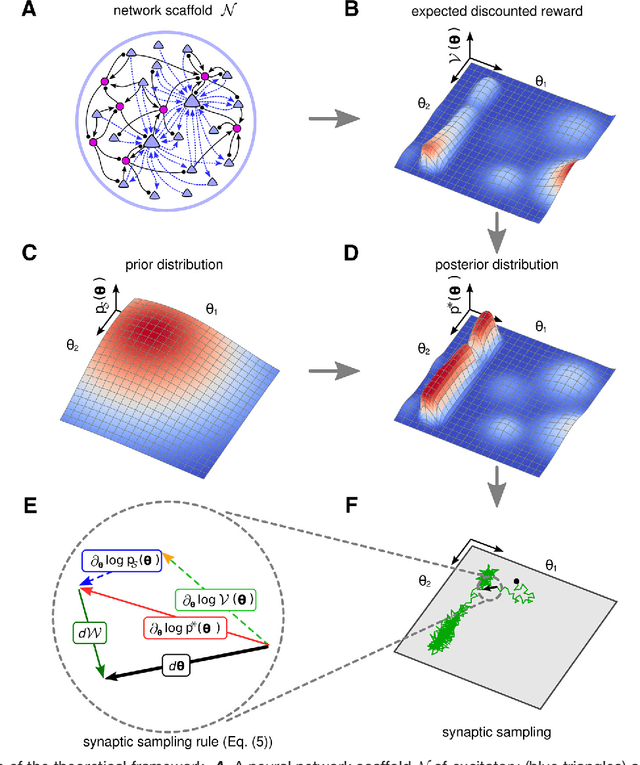
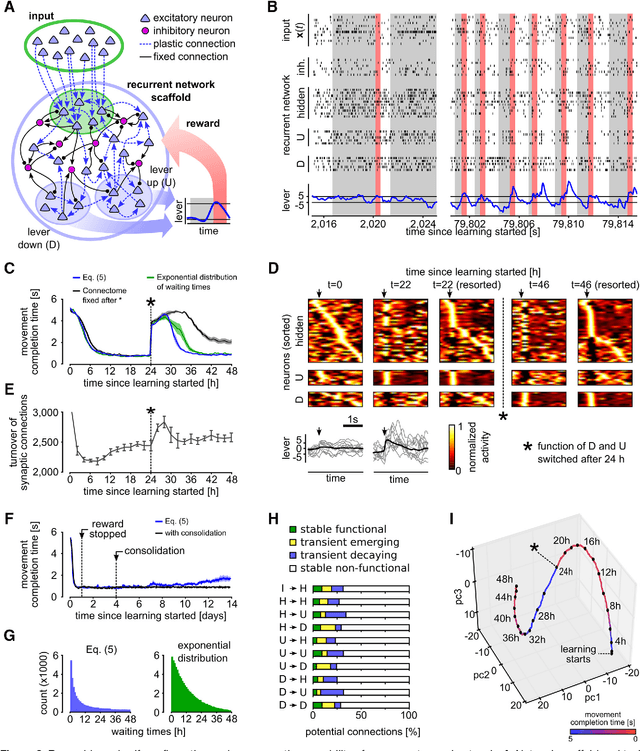
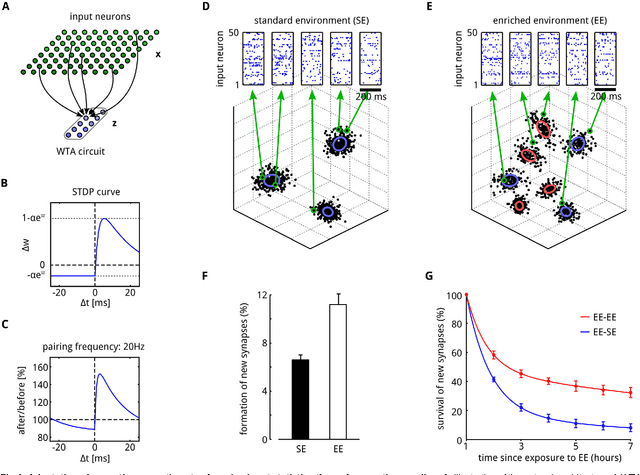
Synaptic connections between neurons in the brain are dynamic because of continuously ongoing spine dynamics, axonal sprouting, and other processes. In fact, it was recently shown that the spontaneous synapse-autonomous component of spine dynamics is at least as large as the component that depends on the history of pre- and postsynaptic neural activity. These data are inconsistent with common models for network plasticity, and raise the questions how neural circuits can maintain a stable computational function in spite of these continuously ongoing processes, and what functional uses these ongoing processes might have. Here, we present a rigorous theoretical framework for these seemingly stochastic spine dynamics and rewiring processes in the context of reward-based learning tasks. We show that spontaneous synapse-autonomous processes, in combination with reward signals such as dopamine, can explain the capability of networks of neurons in the brain to configure themselves for specific computational tasks, and to compensate automatically for later changes in the network or task. Furthermore we show theoretically and through computer simulations that stable computational performance is compatible with continuously ongoing synapse-autonomous changes. After reaching good computational performance it causes primarily a slow drift of network architecture and dynamics in task-irrelevant dimensions, as observed for neural activity in motor cortex and other areas. On the more abstract level of reinforcement learning the resulting model gives rise to an understanding of reward-driven network plasticity as continuous sampling of network configurations.

Network Plasticity as Bayesian Inference

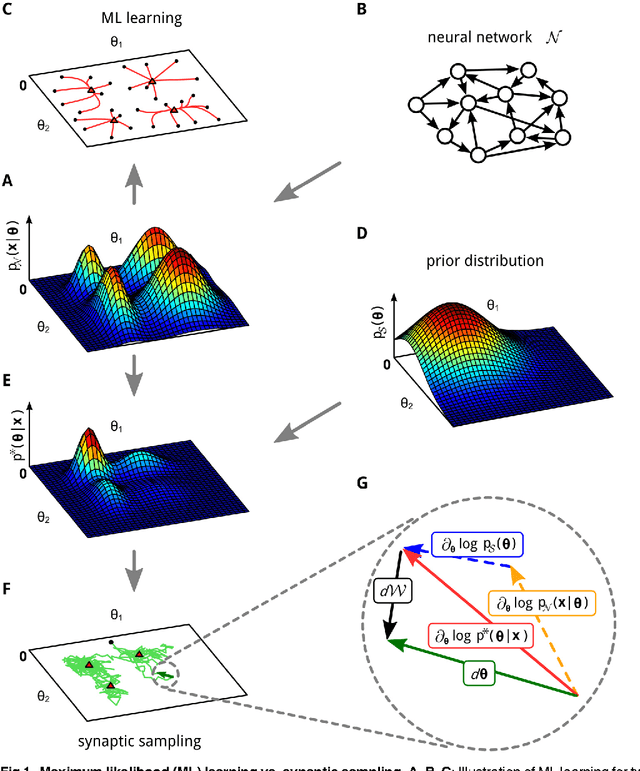
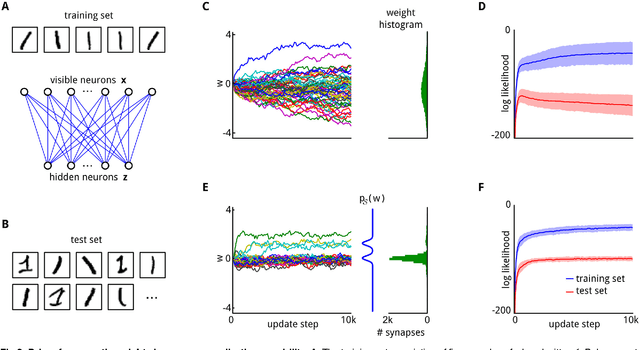
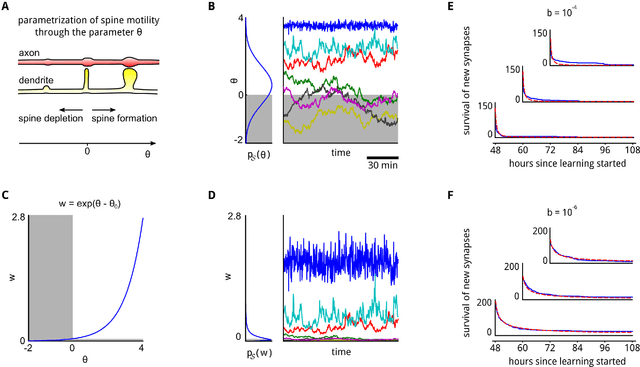
General results from statistical learning theory suggest to understand not only brain computations, but also brain plasticity as probabilistic inference. But a model for that has been missing. We propose that inherently stochastic features of synaptic plasticity and spine motility enable cortical networks of neurons to carry out probabilistic inference by sampling from a posterior distribution of network configurations. This model provides a viable alternative to existing models that propose convergence of parameters to maximum likelihood values. It explains how priors on weight distributions and connection probabilities can be merged optimally with learned experience, how cortical networks can generalize learned information so well to novel experiences, and how they can compensate continuously for unforeseen disturbances of the network. The resulting new theory of network plasticity explains from a functional perspective a number of experimental data on stochastic aspects of synaptic plasticity that previously appeared to be quite puzzling.

A theoretical basis for efficient computations with noisy spiking neurons

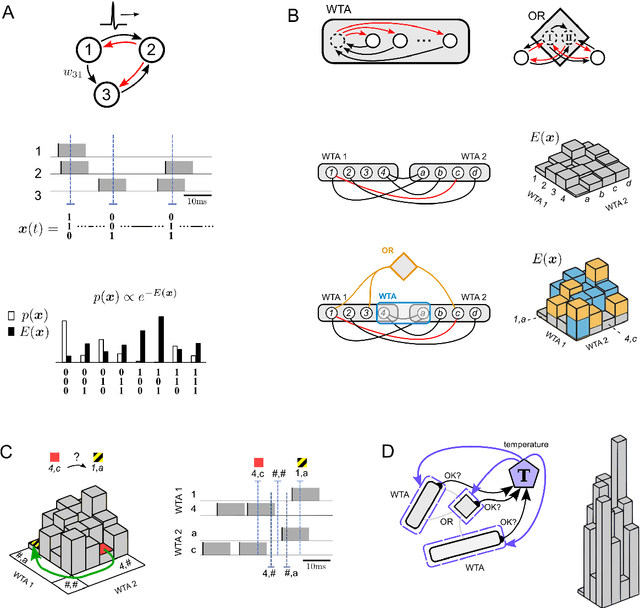
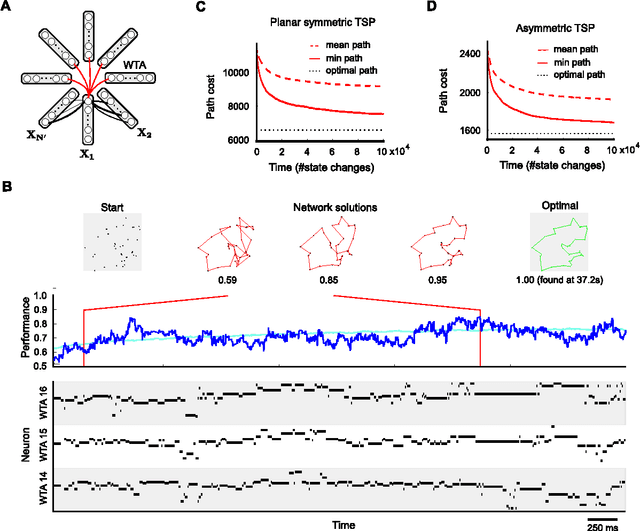
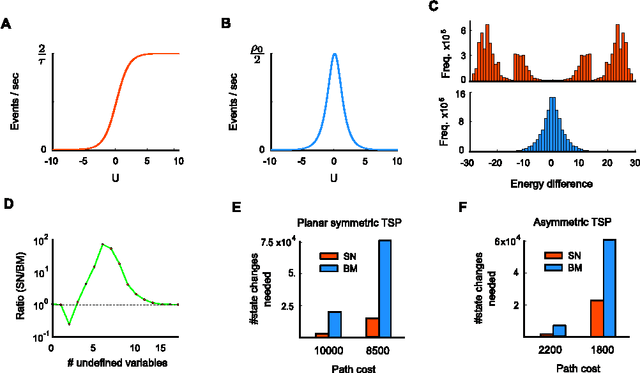
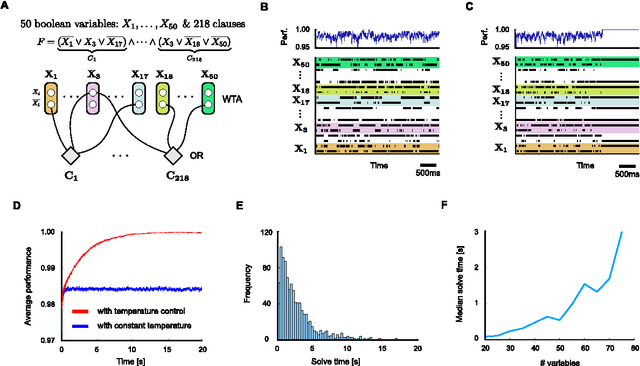
Network of neurons in the brain apply - unlike processors in our current generation of computer hardware - an event-based processing strategy, where short pulses (spikes) are emitted sparsely by neurons to signal the occurrence of an event at a particular point in time. Such spike-based computations promise to be substantially more power-efficient than traditional clocked processing schemes. However it turned out to be surprisingly difficult to design networks of spiking neurons that are able to carry out demanding computations. We present here a new theoretical framework for organizing computations of networks of spiking neurons. In particular, we show that a suitable design enables them to solve hard constraint satisfaction problems from the domains of planning - optimization and verification - logical inference. The underlying design principles employ noise as a computational resource. Nevertheless the timing of spikes (rather than just spike rates) plays an essential role in the resulting computations. Furthermore, one can demonstrate for the Traveling Salesman Problem a surprising computational advantage of networks of spiking neurons compared with traditional artificial neural networks and Gibbs sampling. The identification of such advantage has been a well-known open problem.