Uniform Circle Formation By Oblivious Swarm Robots

In this paper, we study the circle formation problem by multiple autonomous and homogeneous disc-shaped robots (also known as fat robots). The goal of the robots is to place themselves on the periphery of a circle. Circle formation has many real-world applications, such as boundary surveillance. This paper addresses one variant of such problem { uniform circle formation, where the robots have to be equidistant apart. The robots operate by executing cycles of the states wait-look-compute-move. They are oblivious, indistinguishable, anonymous, and do not communicate via message passing. First, we solve the uniform circle formation problem while assuming the robots to be transparent. Next, we address an even weaker model, where the robots are non-transparent and have limited visibility. We propose novel distributed algorithms to solve these variants. Our presented algorithms in this paper are proved to be correct and guarantee to prevent collision and deadlock among the swarm of robots.

Uniform Scattering of Robots on Alternate Nodes of a Grid

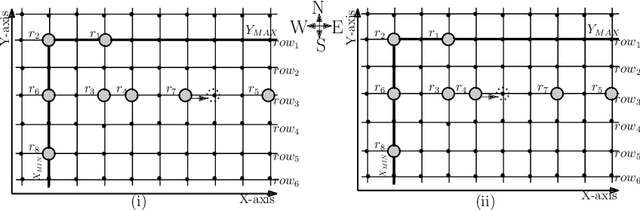
In this paper, we propose a distributed algorithm to uniformly scatter the robots along a grid, with robots on alternate nodes of this grid distribution. These homogeneous, autonomous mobile robots place themselves equidistant apart on the grid, which can be required for guarding or covering a geographical area by the robots. The robots operate by executing cycles of the states "look-compute-move". In the look phase, it looks to see the position of the other robots; in the compute phase, it computes a destination to move to; and then in the move phase, it moves to that computed destination. They do not interact by message passing and can recollect neither the past actions nor the looked data from the previous cycle, i.e., oblivious. The robots are semi-synchronous, anonymous and have unlimited visibility. Eventually, the robots uniformly distribute themselves on alternate nodes of a grid, leaving the adjacent nodes of the grid vacant. The algorithm presented also assures no collision or deadlock among the robots.

A Get-Together for Deaf and Dumb Robots in Three dimensional Space

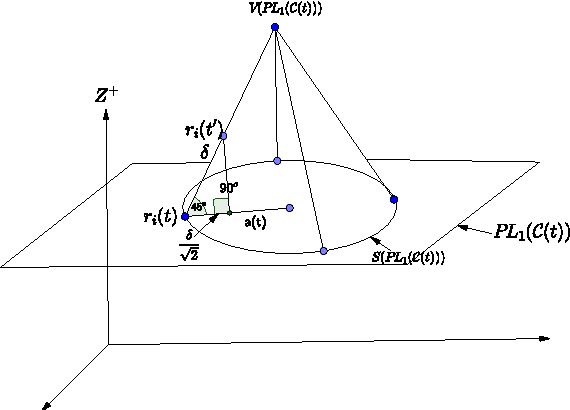
This paper proposes a strategy for a group of deaf and dumb robots, carrying clocks from different countries, to meet at a geographical location which is not fixed in advanced. The robots act independently. They can observe others, compute some locations and walk towards those locations. They can only get a snapshot of the locations of other robots but can not detect whether they are static or in motion. The robots are forgetful; once they have completed their motion they forget their previous locations and observations. Again they decide new destinations to move to. Eventually all the robots compute the same destination and meet there. There exists no global positioning system. As they stand, they agree on up and down directions. However, as they do not have any compass, the other directions are not agreed upon. They also do not agree on the clockwise direction. For determining a strategy, we imagine the robots to be points on a three dimensional plane where all the robots are mutually visible to each other always. The strategy we propose has to be obeyed by all the robots independently with respect to their own clock and compass. Initially the robots start from distinct locations. Some dead robots may be present in the system or some may die any time before or after the get together. However, the live robots are not aware of the presence of these dead robots.

Pattern Formation for Asynchronous Robots without Agreement in Chirality

This paper presents a deterministic algorithm for forming a given asymmetric pattern in finite time by a set of autonomous, homogeneous, oblivious mobile robots under the CORDA model. The robots are represented as points on the 2D plane. There is no explicit communication between the robots. The robots coordinate among themselves by observing the positions of the other robots on the plane. Initially all the robots are assumed to be stationary. The robots have local coordinate systems defined by Sense of Direction (SoD), orientation or chirality and scale. Initially the robots are in asymmetric configuration. We show that these robots can form any given asymmetric pattern in finite time.