CryoBench: Diverse and challenging datasets for the heterogeneity problem in cryo-EM

Cryo-electron microscopy (cryo-EM) is a powerful technique for determining high-resolution 3D biomolecular structures from imaging data. As this technique can capture dynamic biomolecular complexes, 3D reconstruction methods are increasingly being developed to resolve this intrinsic structural heterogeneity. However, the absence of standardized benchmarks with ground truth structures and validation metrics limits the advancement of the field. Here, we propose CryoBench, a suite of datasets, metrics, and performance benchmarks for heterogeneous reconstruction in cryo-EM. We propose five datasets representing different sources of heterogeneity and degrees of difficulty. These include conformational heterogeneity generated from simple motions and random configurations of antibody complexes and from tens of thousands of structures sampled from a molecular dynamics simulation. We also design datasets containing compositional heterogeneity from mixtures of ribosome assembly states and 100 common complexes present in cells. We then perform a comprehensive analysis of state-of-the-art heterogeneous reconstruction tools including neural and non-neural methods and their sensitivity to noise, and propose new metrics for quantitative comparison of methods. We hope that this benchmark will be a foundational resource for analyzing existing methods and new algorithmic development in both the cryo-EM and machine learning communities.

Exploring the Adjugate Matrix Approach to Quaternion Pose Extraction

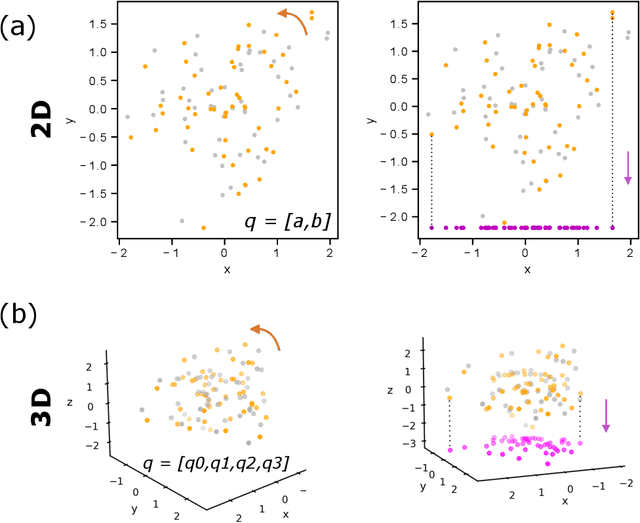
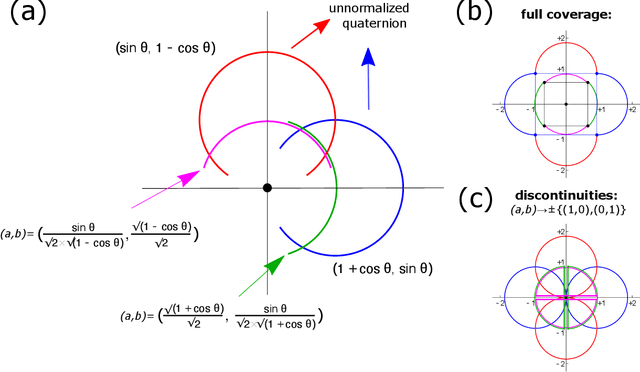
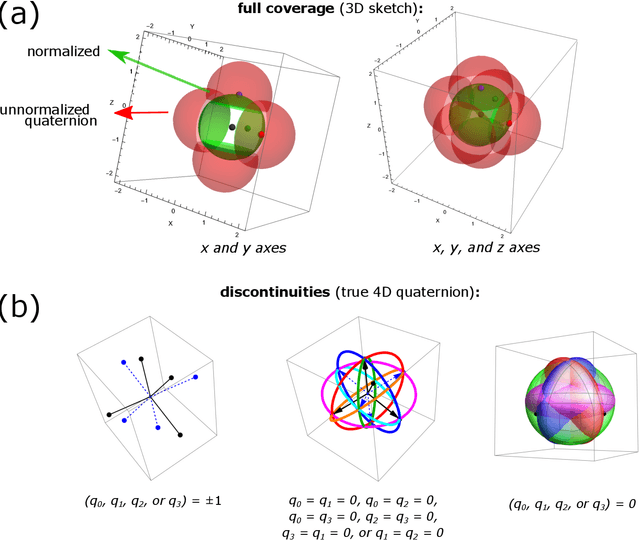
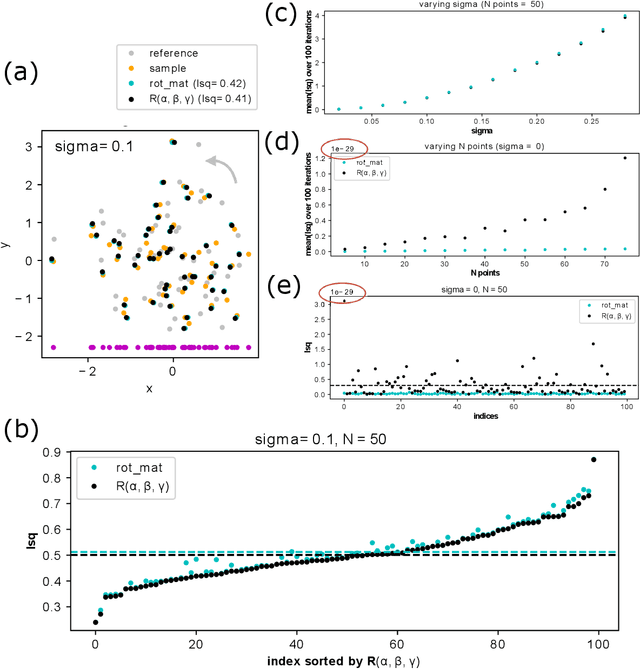
Quaternions are important for a wide variety of rotation-related problems in computer graphics, machine vision, and robotics. We study the nontrivial geometry of the relationship between quaternions and rotation matrices by exploiting the adjugate matrix of the characteristic equation of a related eigenvalue problem to obtain the manifold of the space of a quaternion eigenvector. We argue that quaternions parameterized by their corresponding rotation matrices cannot be expressed, for example, in machine learning tasks, as single-valued functions: the quaternion solution must instead be treated as a manifold, with different algebraic solutions for each of several single-valued sectors represented by the adjugate matrix. We conclude with novel constructions exploiting the quaternion adjugate variables to revisit several classic pose estimation applications: 2D point-cloud matching, 2D point-cloud-to-projection matching, 3D point-cloud matching, 3D orthographic point-cloud-to-projection matching, and 3D perspective point-cloud-to-projection matching. We find an exact solution to the 3D orthographic least squares pose extraction problem, and apply it successfully also to the perspective pose extraction problem with results that improve on existing methods.