Reliability Analysis of Complex Systems using Subset Simulations with Hamiltonian Neural Networks

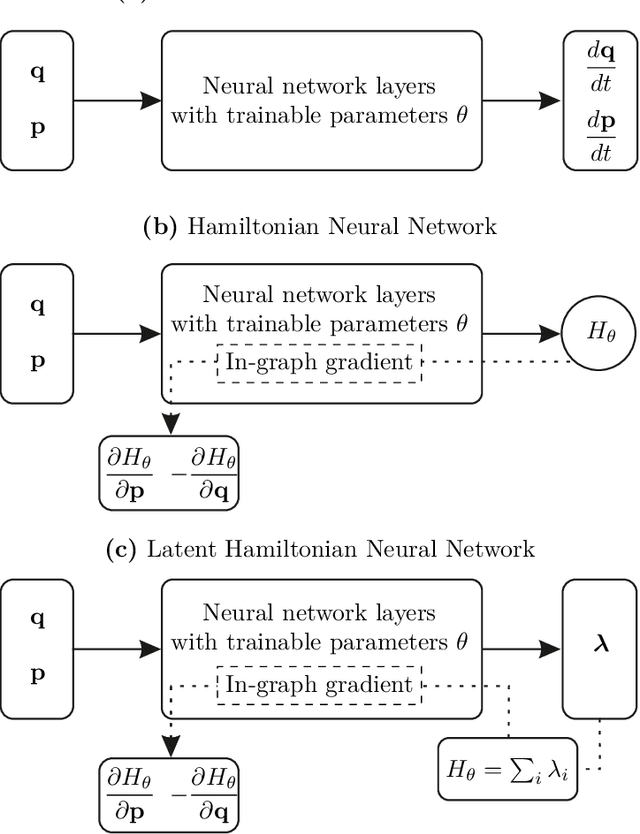
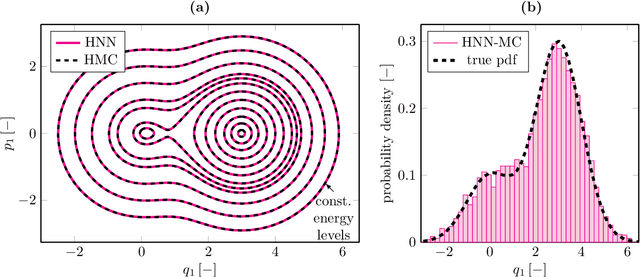
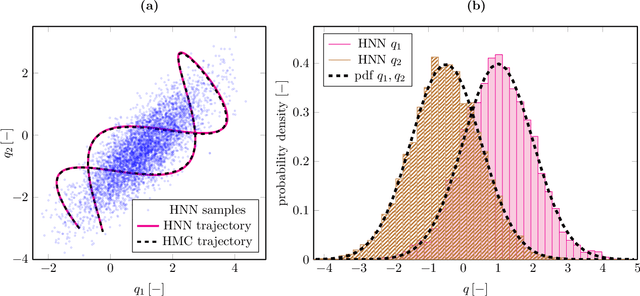
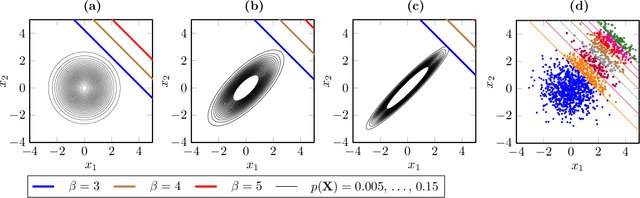
We present a new Subset Simulation approach using Hamiltonian neural network-based Monte Carlo sampling for reliability analysis. The proposed strategy combines the superior sampling of the Hamiltonian Monte Carlo method with computationally efficient gradient evaluations using Hamiltonian neural networks. This combination is especially advantageous because the neural network architecture conserves the Hamiltonian, which defines the acceptance criteria of the Hamiltonian Monte Carlo sampler. Hence, this strategy achieves high acceptance rates at low computational cost. Our approach estimates small failure probabilities using Subset Simulations. However, in low-probability sample regions, the gradient evaluation is particularly challenging. The remarkable accuracy of the proposed strategy is demonstrated on different reliability problems, and its efficiency is compared to the traditional Hamiltonian Monte Carlo method. We note that this approach can reach its limitations for gradient estimations in low-probability regions of complex and high-dimensional distributions. Thus, we propose techniques to improve gradient prediction in these particular situations and enable accurate estimations of the probability of failure. The highlight of this study is the reliability analysis of a system whose parameter distributions must be inferred with Bayesian inference problems. In such a case, the Hamiltonian Monte Carlo method requires a full model evaluation for each gradient evaluation and, therefore, comes at a very high cost. However, using Hamiltonian neural networks in this framework replaces the expensive model evaluation, resulting in tremendous improvements in computational efficiency.

General multi-fidelity surrogate models: Framework and active learning strategies for efficient rare event simulation

Estimating the probability of failure for complex real-world systems using high-fidelity computational models is often prohibitively expensive, especially when the probability is small. Exploiting low-fidelity models can make this process more feasible, but merging information from multiple low-fidelity and high-fidelity models poses several challenges. This paper presents a robust multi-fidelity surrogate modeling strategy in which the multi-fidelity surrogate is assembled using an active learning strategy using an on-the-fly model adequacy assessment set within a subset simulation framework for efficient reliability analysis. The multi-fidelity surrogate is assembled by first applying a Gaussian process correction to each low-fidelity model and assigning a model probability based on the model's local predictive accuracy and cost. Three strategies are proposed to fuse these individual surrogates into an overall surrogate model based on model averaging and deterministic/stochastic model selection. The strategies also dictate which model evaluations are necessary. No assumptions are made about the relationships between low-fidelity models, while the high-fidelity model is assumed to be the most accurate and most computationally expensive model. Through two analytical and two numerical case studies, including a case study evaluating the failure probability of Tristructural isotropic-coated (TRISO) nuclear fuels, the algorithm is shown to be highly accurate while drastically reducing the number of high-fidelity model calls (and hence computational cost).

Physics-Informed Machine Learning of Dynamical Systems for Efficient Bayesian Inference

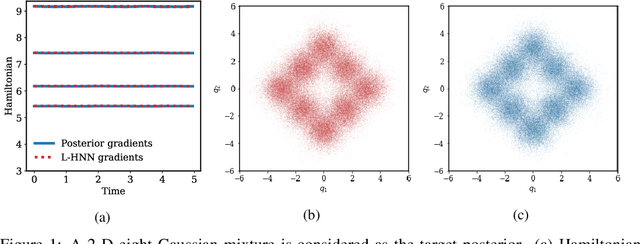
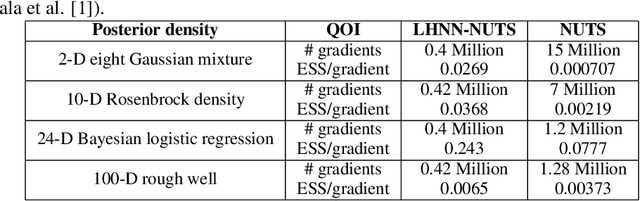
Although the no-u-turn sampler (NUTS) is a widely adopted method for performing Bayesian inference, it requires numerous posterior gradients which can be expensive to compute in practice. Recently, there has been a significant interest in physics-based machine learning of dynamical (or Hamiltonian) systems and Hamiltonian neural networks (HNNs) is a noteworthy architecture. But these types of architectures have not been applied to solve Bayesian inference problems efficiently. We propose the use of HNNs for performing Bayesian inference efficiently without requiring numerous posterior gradients. We introduce latent variable outputs to HNNs (L-HNNs) for improved expressivity and reduced integration errors. We integrate L-HNNs in NUTS and further propose an online error monitoring scheme to prevent sampling degeneracy in regions where L-HNNs may have little training data. We demonstrate L-HNNs in NUTS with online error monitoring considering several complex high-dimensional posterior densities and compare its performance to NUTS.

Bayesian Inference with Latent Hamiltonian Neural Networks

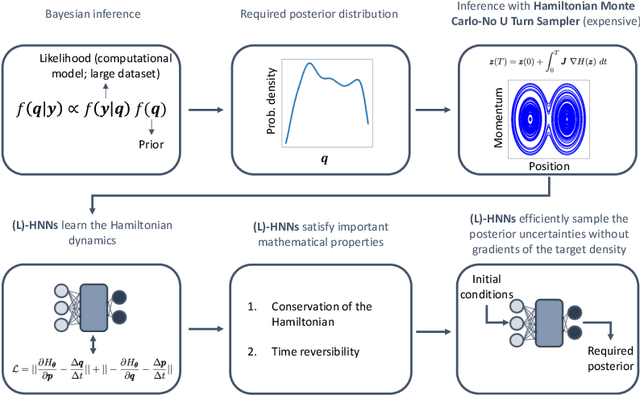
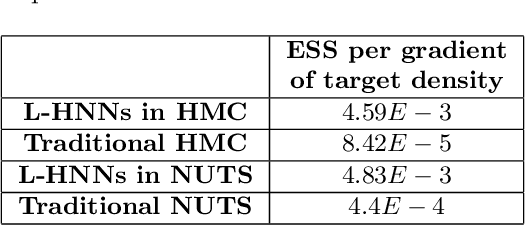
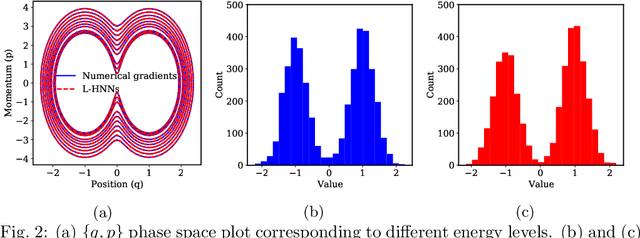
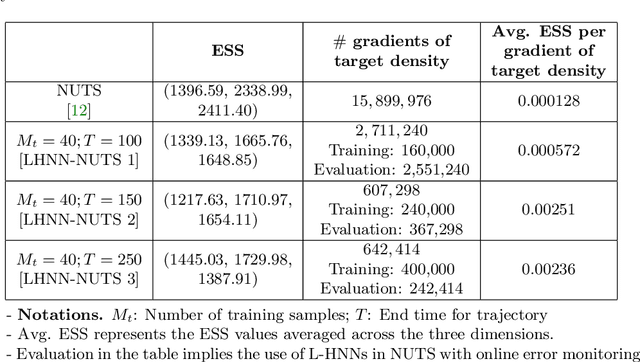
When sampling for Bayesian inference, one popular approach is to use Hamiltonian Monte Carlo (HMC) and specifically the No-U-Turn Sampler (NUTS) which automatically decides the end time of the Hamiltonian trajectory. However, HMC and NUTS can require numerous numerical gradients of the target density, and can prove slow in practice. We propose Hamiltonian neural networks (HNNs) with HMC and NUTS for solving Bayesian inference problems. Once trained, HNNs do not require numerical gradients of the target density during sampling. Moreover, they satisfy important properties such as perfect time reversibility and Hamiltonian conservation, making them well-suited for use within HMC and NUTS because stationarity can be shown. We also propose an HNN extension called latent HNNs (L-HNNs), which are capable of predicting latent variable outputs. Compared to HNNs, L-HNNs offer improved expressivity and reduced integration errors. Finally, we employ L-HNNs in NUTS with an online error monitoring scheme to prevent sample degeneracy in regions of low probability density. We demonstrate L-HNNs in NUTS with online error monitoring on several examples involving complex, heavy-tailed, and high-local-curvature probability densities. Overall, L-HNNs in NUTS with online error monitoring satisfactorily inferred these probability densities. Compared to traditional NUTS, L-HNNs in NUTS with online error monitoring required 1--2 orders of magnitude fewer numerical gradients of the target density and improved the effective sample size (ESS) per gradient by an order of magnitude.

Efficient Interdependent Systems Recovery Modeling with DeepONets

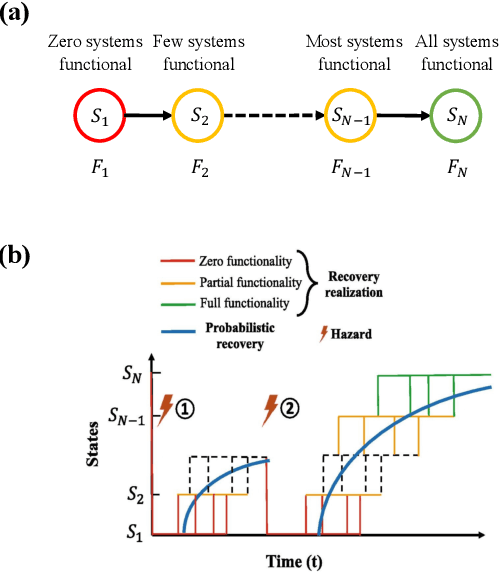
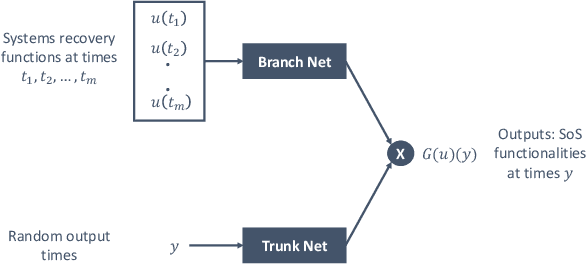
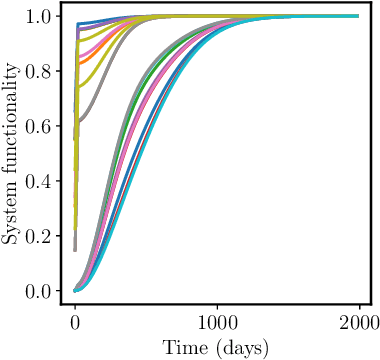
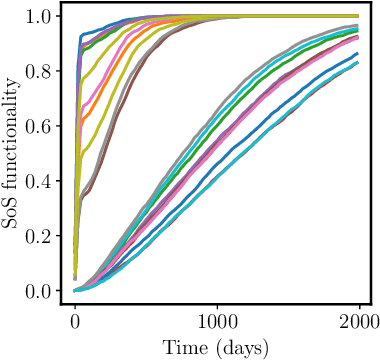
Modeling the recovery of interdependent critical infrastructure is a key component of quantifying and optimizing societal resilience to disruptive events. However, simulating the recovery of large-scale interdependent systems under random disruptive events is computationally expensive. Therefore, we propose the application of Deep Operator Networks (DeepONets) in this paper to accelerate the recovery modeling of interdependent systems. DeepONets are ML architectures which identify mathematical operators from data. The form of governing equations DeepONets identify and the governing equation of interdependent systems recovery model are similar. Therefore, we hypothesize that DeepONets can efficiently model the interdependent systems recovery with little training data. We applied DeepONets to a simple case of four interdependent systems with sixteen states. DeepONets, overall, performed satisfactorily in predicting the recovery of these interdependent systems for out of training sample data when compared to reference results.

Reliability Estimation of an Advanced Nuclear Fuel using Coupled Active Learning, Multifidelity Modeling, and Subset Simulation

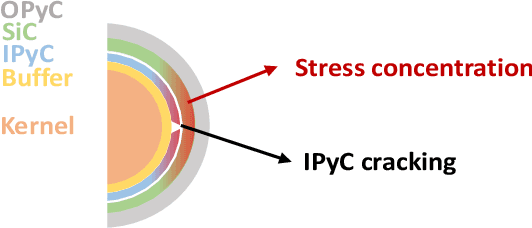
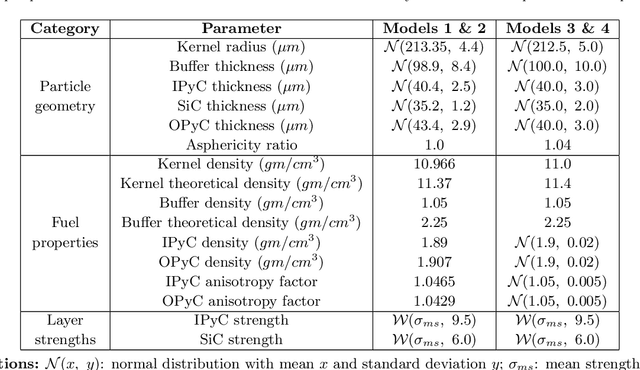
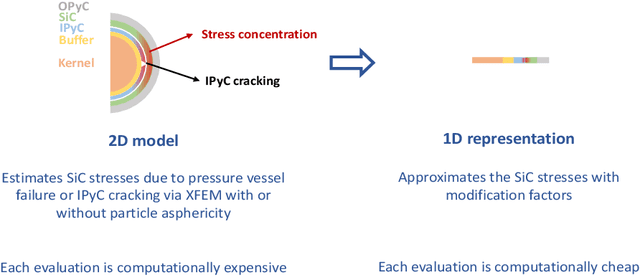
Tristructural isotropic (TRISO)-coated particle fuel is a robust nuclear fuel and determining its reliability is critical for the success of advanced nuclear technologies. However, TRISO failure probabilities are small and the associated computational models are expensive. We used coupled active learning, multifidelity modeling, and subset simulation to estimate the failure probabilities of TRISO fuels using several 1D and 2D models. With multifidelity modeling, we replaced expensive high-fidelity (HF) model evaluations with information fusion from two low-fidelity (LF) models. For the 1D TRISO models, we considered three multifidelity modeling strategies: only Kriging, Kriging LF prediction plus Kriging correction, and deep neural network (DNN) LF prediction plus Kriging correction. While the results across these multifidelity modeling strategies compared satisfactorily, strategies employing information fusion from two LF models consistently called the HF model least often. Next, for the 2D TRISO model, we considered two multifidelity modeling strategies: DNN LF prediction plus Kriging correction (data-driven) and 1D TRISO LF prediction plus Kriging correction (physics-based). The physics-based strategy, as expected, consistently required the fewest calls to the HF model. However, the data-driven strategy had a lower overall simulation time since the DNN predictions are instantaneous, and the 1D TRISO model requires a non-negligible simulation time.