Bayesian Inference with Latent Hamiltonian Neural Networks
Paper and Code
Aug 12, 2022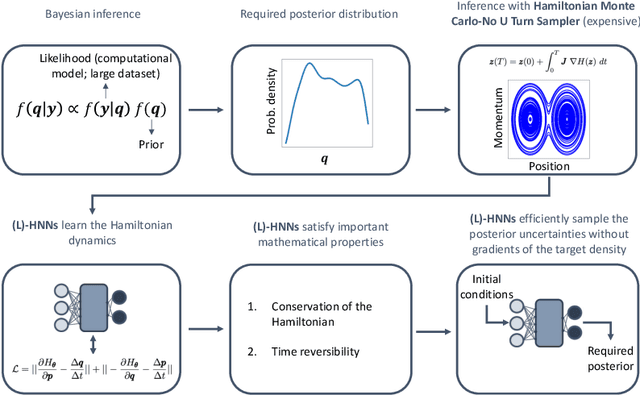
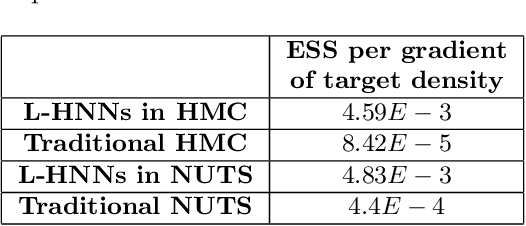
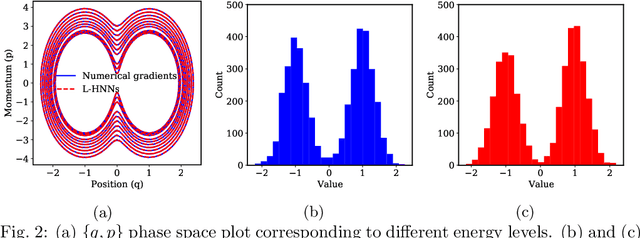
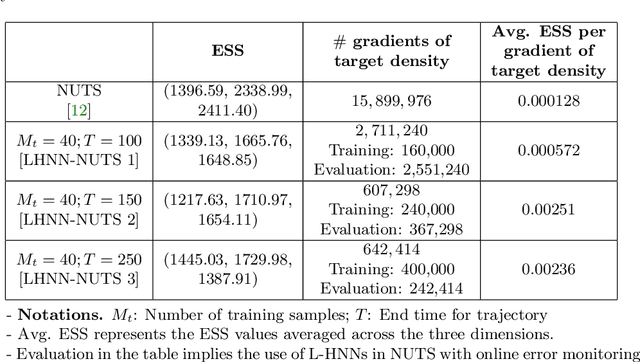
When sampling for Bayesian inference, one popular approach is to use Hamiltonian Monte Carlo (HMC) and specifically the No-U-Turn Sampler (NUTS) which automatically decides the end time of the Hamiltonian trajectory. However, HMC and NUTS can require numerous numerical gradients of the target density, and can prove slow in practice. We propose Hamiltonian neural networks (HNNs) with HMC and NUTS for solving Bayesian inference problems. Once trained, HNNs do not require numerical gradients of the target density during sampling. Moreover, they satisfy important properties such as perfect time reversibility and Hamiltonian conservation, making them well-suited for use within HMC and NUTS because stationarity can be shown. We also propose an HNN extension called latent HNNs (L-HNNs), which are capable of predicting latent variable outputs. Compared to HNNs, L-HNNs offer improved expressivity and reduced integration errors. Finally, we employ L-HNNs in NUTS with an online error monitoring scheme to prevent sample degeneracy in regions of low probability density. We demonstrate L-HNNs in NUTS with online error monitoring on several examples involving complex, heavy-tailed, and high-local-curvature probability densities. Overall, L-HNNs in NUTS with online error monitoring satisfactorily inferred these probability densities. Compared to traditional NUTS, L-HNNs in NUTS with online error monitoring required 1--2 orders of magnitude fewer numerical gradients of the target density and improved the effective sample size (ESS) per gradient by an order of magnitude.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge