Physics-Informed Machine Learning of Dynamical Systems for Efficient Bayesian Inference
Paper and Code
Sep 19, 2022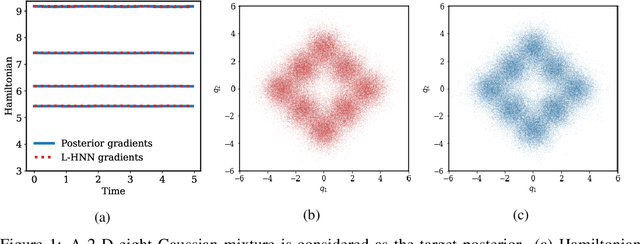
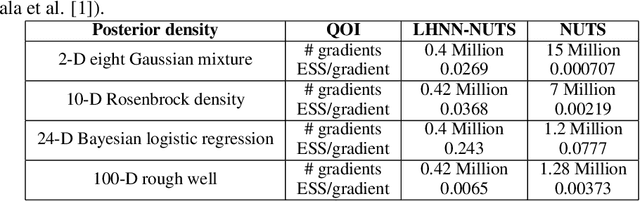
Although the no-u-turn sampler (NUTS) is a widely adopted method for performing Bayesian inference, it requires numerous posterior gradients which can be expensive to compute in practice. Recently, there has been a significant interest in physics-based machine learning of dynamical (or Hamiltonian) systems and Hamiltonian neural networks (HNNs) is a noteworthy architecture. But these types of architectures have not been applied to solve Bayesian inference problems efficiently. We propose the use of HNNs for performing Bayesian inference efficiently without requiring numerous posterior gradients. We introduce latent variable outputs to HNNs (L-HNNs) for improved expressivity and reduced integration errors. We integrate L-HNNs in NUTS and further propose an online error monitoring scheme to prevent sampling degeneracy in regions where L-HNNs may have little training data. We demonstrate L-HNNs in NUTS with online error monitoring considering several complex high-dimensional posterior densities and compare its performance to NUTS.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge