Bernd Markert
Reliability Analysis of Complex Systems using Subset Simulations with Hamiltonian Neural Networks
Jan 10, 2024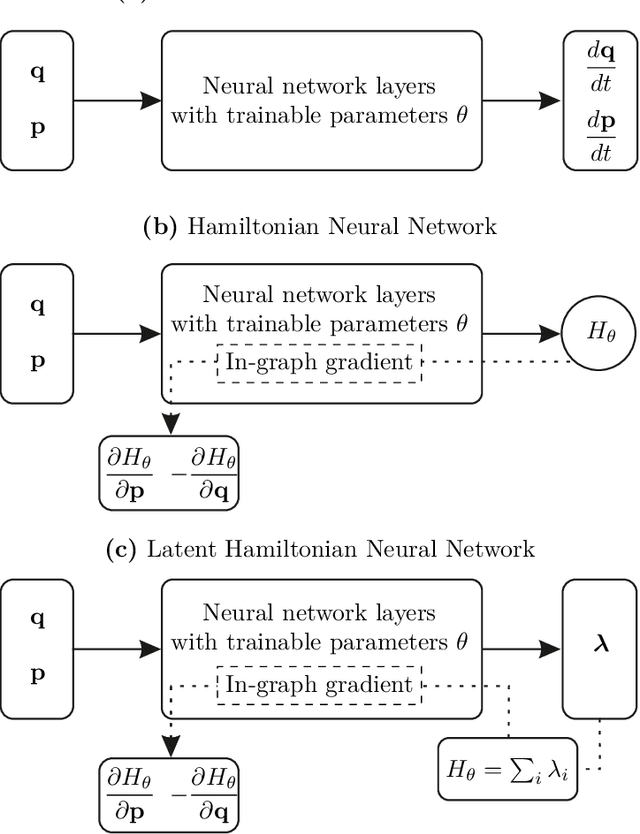
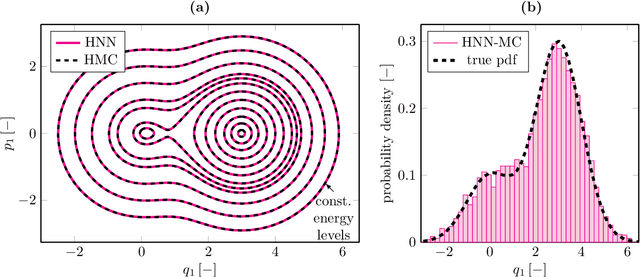
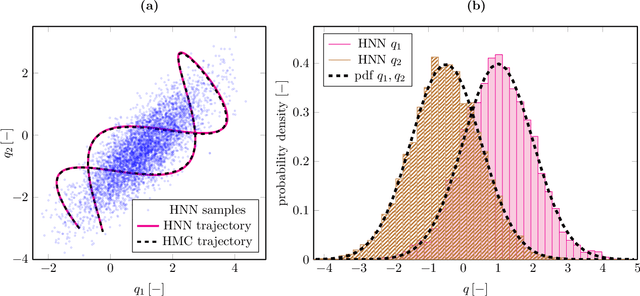
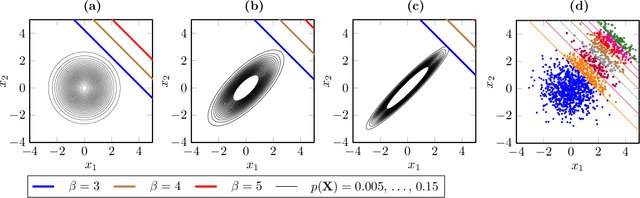
Abstract:We present a new Subset Simulation approach using Hamiltonian neural network-based Monte Carlo sampling for reliability analysis. The proposed strategy combines the superior sampling of the Hamiltonian Monte Carlo method with computationally efficient gradient evaluations using Hamiltonian neural networks. This combination is especially advantageous because the neural network architecture conserves the Hamiltonian, which defines the acceptance criteria of the Hamiltonian Monte Carlo sampler. Hence, this strategy achieves high acceptance rates at low computational cost. Our approach estimates small failure probabilities using Subset Simulations. However, in low-probability sample regions, the gradient evaluation is particularly challenging. The remarkable accuracy of the proposed strategy is demonstrated on different reliability problems, and its efficiency is compared to the traditional Hamiltonian Monte Carlo method. We note that this approach can reach its limitations for gradient estimations in low-probability regions of complex and high-dimensional distributions. Thus, we propose techniques to improve gradient prediction in these particular situations and enable accurate estimations of the probability of failure. The highlight of this study is the reliability analysis of a system whose parameter distributions must be inferred with Bayesian inference problems. In such a case, the Hamiltonian Monte Carlo method requires a full model evaluation for each gradient evaluation and, therefore, comes at a very high cost. However, using Hamiltonian neural networks in this framework replaces the expensive model evaluation, resulting in tremendous improvements in computational efficiency.
Explainable artificial intelligence for mechanics: physics-informing neural networks for constitutive models
May 20, 2021



Abstract:(Artificial) neural networks have become increasingly popular in mechanics as means to accelerate computations with model order reduction techniques and as universal models for a wide variety of materials. However, the major disadvantage of neural networks remains: their numerous parameters are challenging to interpret and explain. Thus, neural networks are often labeled as black boxes, and their results often elude human interpretation. In mechanics, the new and active field of physics-informed neural networks attempts to mitigate this disadvantage by designing deep neural networks on the basis of mechanical knowledge. By using this a priori knowledge, deeper and more complex neural networks became feasible, since the mechanical assumptions could be explained. However, the internal reasoning and explanation of neural network parameters remain mysterious. Complementary to the physics-informed approach, we propose a first step towards a physics-informing approach, which explains neural networks trained on mechanical data a posteriori. This novel explainable artificial intelligence approach aims at elucidating the black box of neural networks and their high-dimensional representations. Therein, the principal component analysis decorrelates the distributed representations in cell states of RNNs and allows the comparison to known and fundamental functions. The novel approach is supported by a systematic hyperparameter search strategy that identifies the best neural network architectures and training parameters. The findings of three case studies on fundamental constitutive models (hyperelasticity, elastoplasticity, and viscoelasticity) imply that the proposed strategy can help identify numerical and analytical closed-form solutions to characterize new materials.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge