Robust real-time imaging through flexible multimode fibers

Conventional endoscopes comprise a bundle of optical fibers, associating one fiber for each pixel in the image. In principle, this can be reduced to a single multimode optical fiber (MMF), the width of a human hair, with one fiber spatial-mode per image pixel. However, images transmitted through a MMF emerge as unrecognisable speckle patterns due to dispersion and coupling between the spatial modes of the fiber. Furthermore, speckle patterns change as the fiber undergoes bending, making the use of MMFs in flexible imaging applications even more complicated. In this paper, we propose a real-time imaging system using flexible MMFs, but which is robust to bending. Our approach does not require access or feedback signal from the distal end of the fiber during imaging. We leverage a variational autoencoder (VAE) to reconstruct and classify images from the speckles and show that these images can still be recovered when the bend configuration of the fiber is changed to one that was not part of the training set. We utilize a MMF $300$ mm long with a 50 $\mu$m core for imaging $10\times 10$ cm objects placed approximately at $20$ cm from the fiber and the system can deal with a change in fiber bend of 50$^\circ$ and range of movement of 8 cm.

Bessel Equivariant Networks for Inversion of Transmission Effects in Multi-Mode Optical Fibres

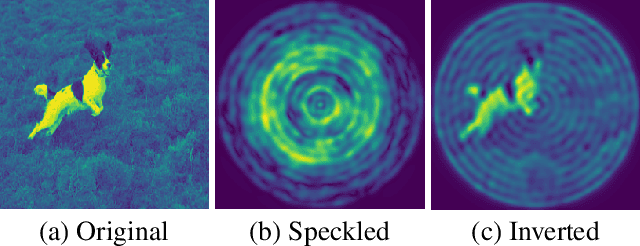
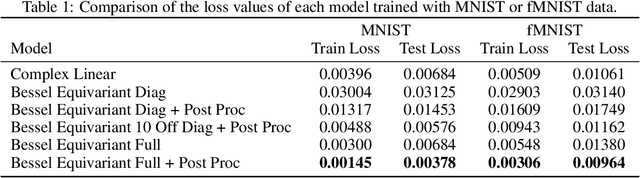
We develop a new type of model for solving the task of inverting the transmission effects of multi-mode optical fibres through the construction of an $\mathrm{SO}^{+}(2,1)$-equivariant neural network. This model takes advantage of the of the azimuthal correlations known to exist in fibre speckle patterns and naturally accounts for the difference in spatial arrangement between input and speckle patterns. In addition, we use a second post-processing network to remove circular artifacts, fill gaps, and sharpen the images, which is required due to the nature of optical fibre transmission. This two stage approach allows for the inspection of the predicted images produced by the more robust physically motivated equivariant model, which could be useful in a safety-critical application, or by the output of both models, which produces high quality images. Further, this model can scale to previously unachievable resolutions of imaging with multi-mode optical fibres and is demonstrated on $256 \times 256$ pixel images. This is a result of improving the trainable parameter requirement from $\mathcal{O}(N^4)$ to $\mathcal{O}(m)$, where $N$ is pixel size and $m$ is number of fibre modes. Finally, this model generalises to new images, outside of the set of training data classes, better than previous models.