Invariant Smoothing with low process noise

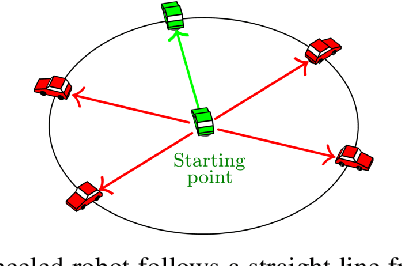
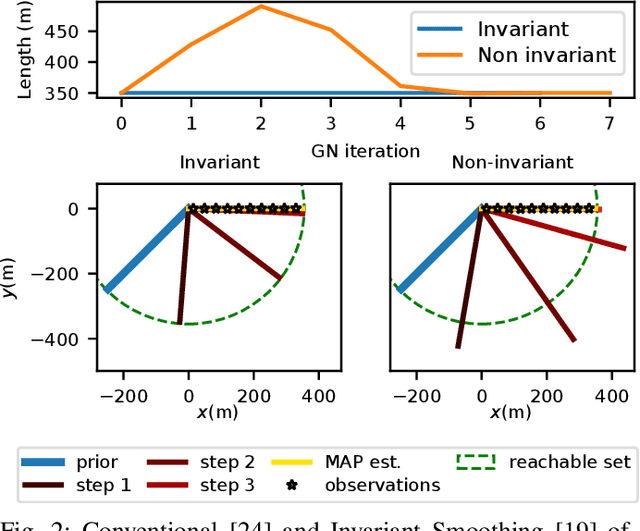
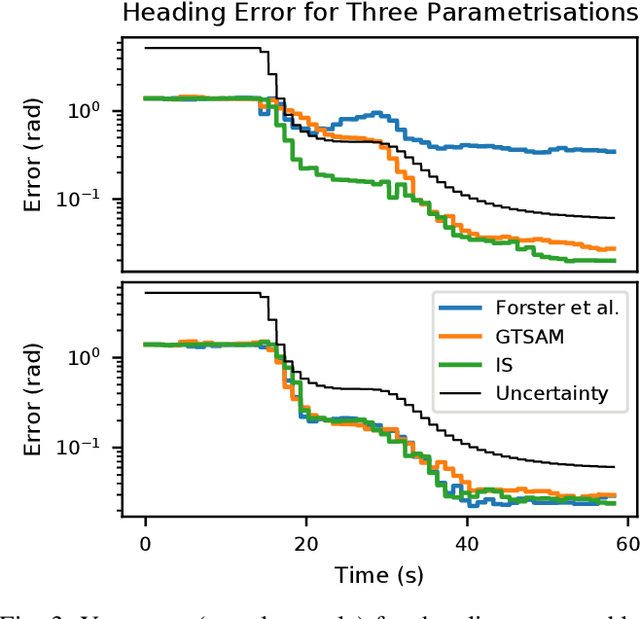
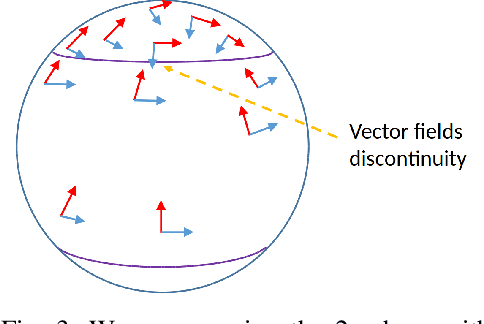
In this paper we address smoothing-that is, optimisation-based-estimation techniques for localisation problems in the case where motion sensors are very accurate. Our mathematical analysis focuses on the difficult limit case where motion sensors are infinitely precise, resulting in the absence of process noise. Then the formulation degenerates, as the dynamical model that serves as a soft constraint becomes an equality constraint, and conventional smoothing methods are not able to fully respect it. By contrast, once an appropriate Lie group embedding has been found, we prove theoretically that invariant smoothing gracefully accommodates this limit case in that the estimates tend to be consistent with the induced constraints when the noise tends to zero. Simulations on the important problem of initial alignement in inertial navigation show that, in a low noise setting, invariant smoothing may favorably compare to state-of-the-art smoothers when using precise inertial measurements units (IMU).

The Geometry of Navigation Problems

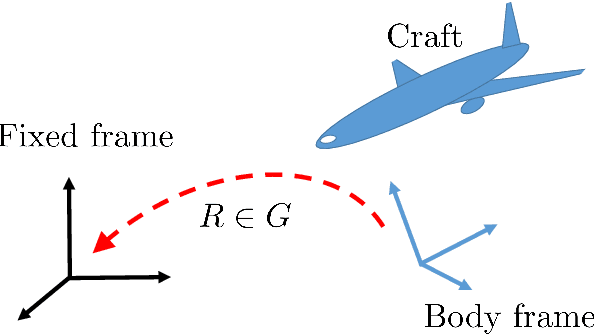
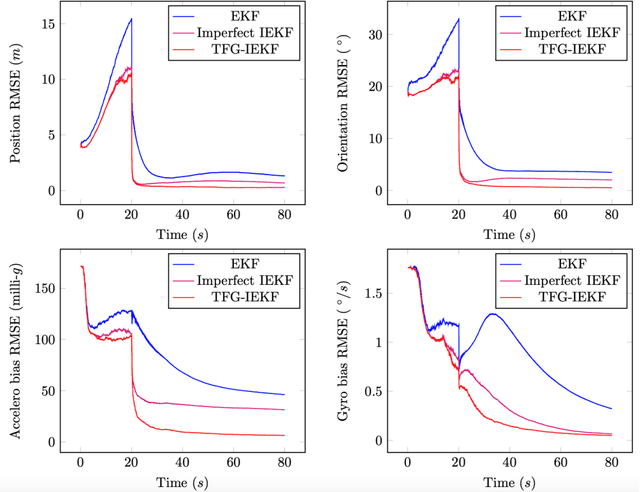
While many works exploiting an existing Lie group structure have been proposed for state estimation, in particular the Invariant Extended Kalman Filter (IEKF), few papers address the construction of a group structure that allows casting a given system into the framework of invariant filtering. In this paper we introduce a large class of systems encompassing most problems involving a navigating vehicle encountered in practice. For those systems we introduce a novel methodology that systematically provides a group structure for the state space, including vectors of the body frame such as biases. We use it to derive observers having properties akin to those of linear observers or filters. The proposed unifying and versatile framework encompasses all systems where IEKF has proved successful, improves state-of-the art "imperfect" IEKF for inertial navigation with sensor biases, and allows addressing novel examples, like GNSS antenna lever arm estimation.

A Code for Unscented Kalman Filtering on Manifolds

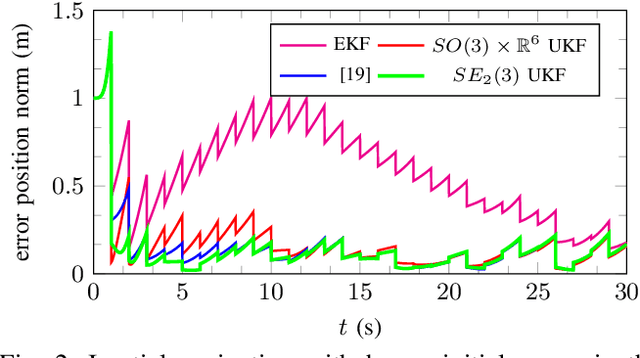
The present paper introduces a novel methodology for Unscented Kalman Filtering (UKF) on manifolds that extends previous work by the authors on UKF on Lie groups. Beyond filtering performance, the main interests of the approach are its versatility, as the method applies to numerous state estimation problems, and its simplicity of implementation for practitioners not being necessarily familiar with manifolds and Lie groups. We have developed the method on two independent open-source Python and Matlab frameworks we call UKF-M, for quickly implementing and testing the approach. The online repositories contain tutorials, documentation, and various relevant robotics examples that the user can readily reproduce and then adapt, for fast prototyping and benchmarking. The code is available at https://github.com/CAOR-MINES-ParisTech/ukfm.

A Mathematical Framework for IMU Error Propagation with Applications to Preintegration

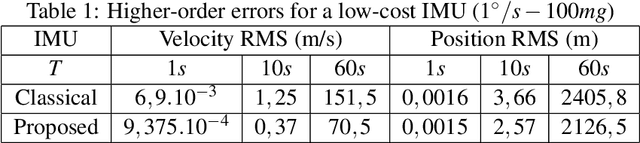
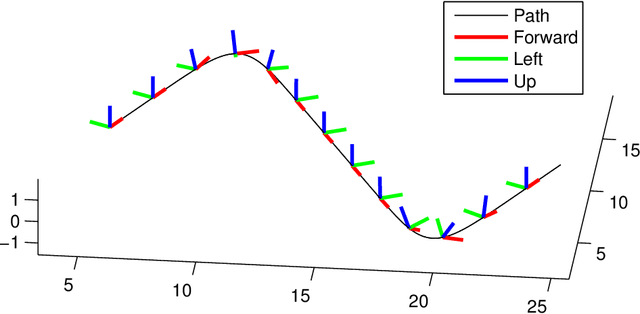
To fuse information from inertial measurement units (IMU) with other sensors one needs an accurate model for IMU error propagation in terms of position, velocity and orientation, a triplet we call extended pose. In this paper we leverage a nontrivial result, namely log-linearity of inertial navigation equations based on the recently introduced Lie group $SE_2(3)$, to transpose the recent methodology of Barfoot and Furgale for associating uncertainty with poses (position, orientation) of $SE(3)$ when using noisy wheel speeds, to the case of extended poses (position, velocity, orientation) of $SE_2(3)$ when using noisy IMUs. Besides, our approach to extended poses combined with log-linearity property allows revisiting the theory of preintegration on manifolds and reaching a further theoretic level in this field. We show exact preintegration formulas that account for rotating Earth, that is, centrifugal force and Coriolis effect, may be derived as a byproduct.

Denoising IMU Gyroscopes with Deep Learning for Open-Loop Attitude Estimation

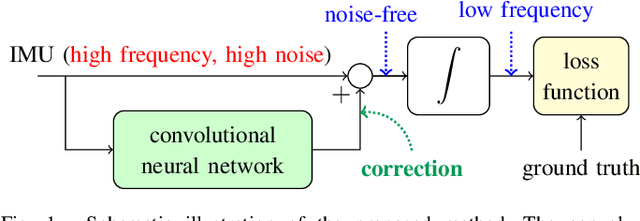
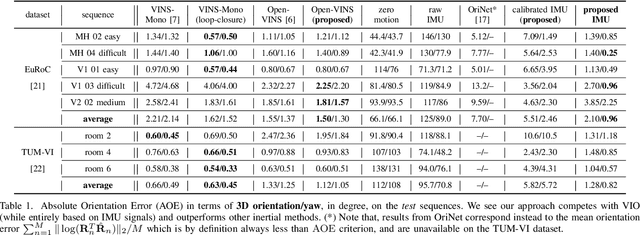
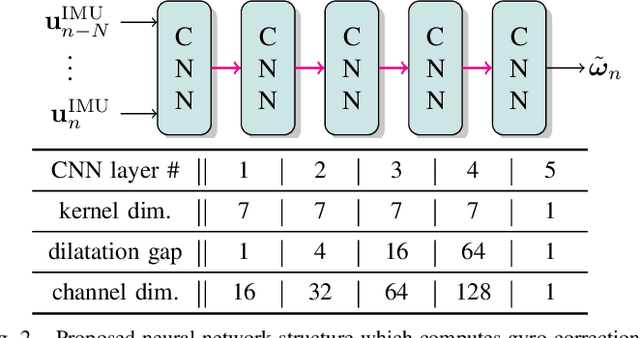
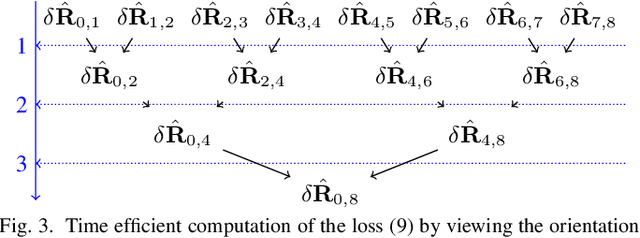
This paper proposes a learning method for denois-ing gyroscopes of Inertial Measurement Units (IMUs) using ground truth data, to estimate in real time the orientation (attitude) of a robot in dead reckoning. The obtained algorithm outperforms the state-of-the-art on the (unseen) test sequences. The obtained performances are achieved thanks to a well chosen model, a proper loss function for orientation increments, and through the identification of key points when training with high-frequency inertial data. Our approach builds upon a neural network based on dilated convolutions, without requiring any recurrent neural network. We demonstrate how efficient our strategy is for 3D attitude estimation on the EuRoC and TUM-VI datasets. Interestingly, we observe our dead reckoning algorithm manages to beat top-ranked visual-inertial odometry systems in terms of attitude estimation although it does not use vision sensors. We believe this paper offers new perspectives for visual-inertial localization and constitutes a step toward more efficient learning methods involving IMUs. Our open-source implementation is available at https://github.com/ mbrossar/denoise-imu-gyro.

RINS-W: Robust Inertial Navigation System on Wheels

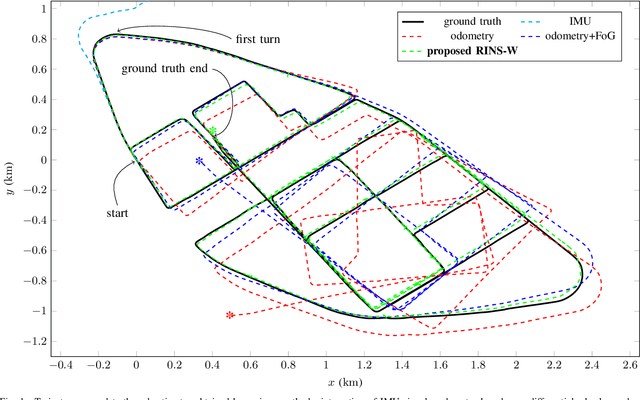
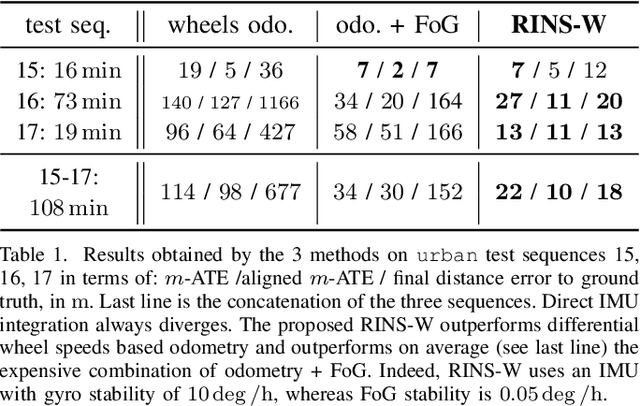
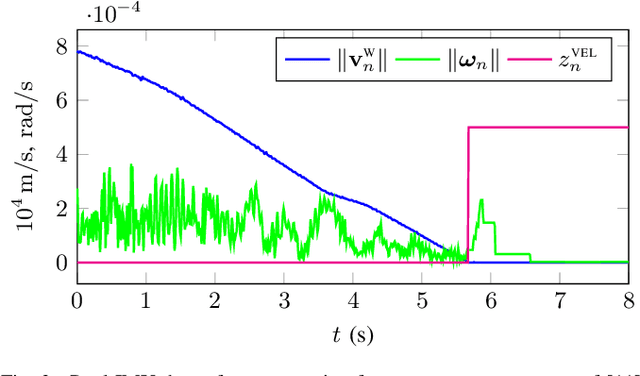
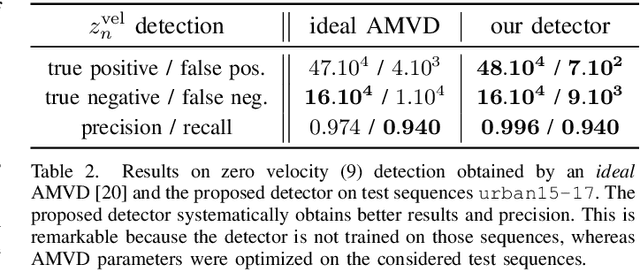
This paper proposes a real-time approach for long-term inertial navigation based only on an Inertial Measurement Unit (IMU) for self-localizing wheeled robots. The approach builds upon two components: 1) a robust detector that uses recurrent deep neural networks to dynamically detect a variety of situations of interest, such as zero velocity or no lateral slip; and 2) a state-of-the-art Kalman filter which incorporates this knowledge as pseudo-measurements for localization. Evaluations on a publicly available car dataset demonstrates that the proposed scheme may achieve a final precision of 20 m for a 21 km long trajectory of a vehicle driving for over an hour, equipped with an IMU of moderate precision (the gyro drift rate is 10 deg/h). To our knowledge, this is the first paper which combines sophisticated deep learning techniques with state-of-the-art filtering methods for pure inertial navigation on wheeled vehicles and as such opens up for novel data-driven inertial navigation techniques. Moreover, albeit taylored for IMU-only based localization, our method may be used as a component for self-localization of wheeled robots equipped with a more complete sensor suite.

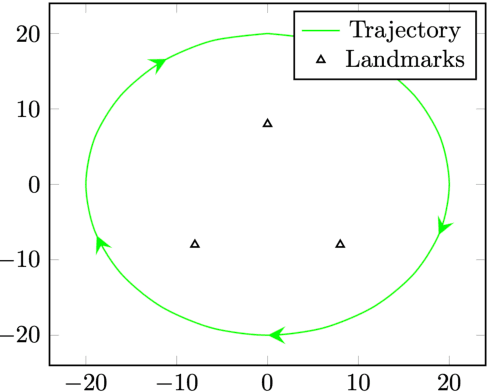
An EKF-SLAM algorithm with consistency properties

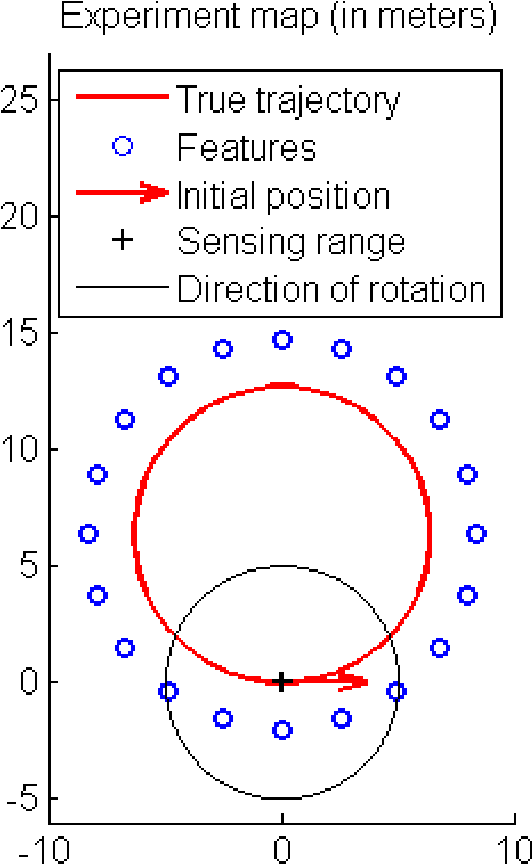
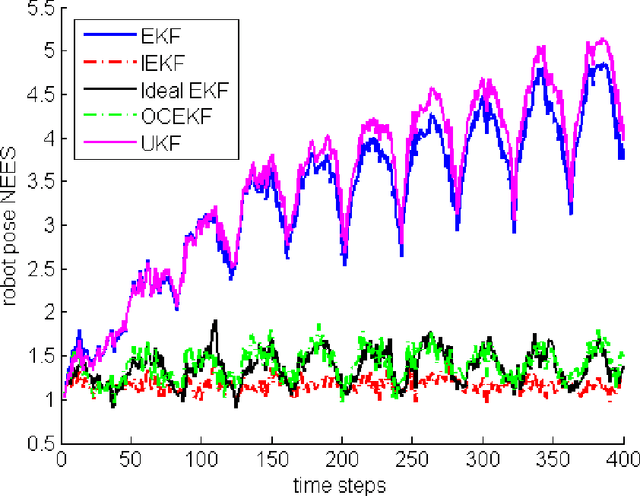
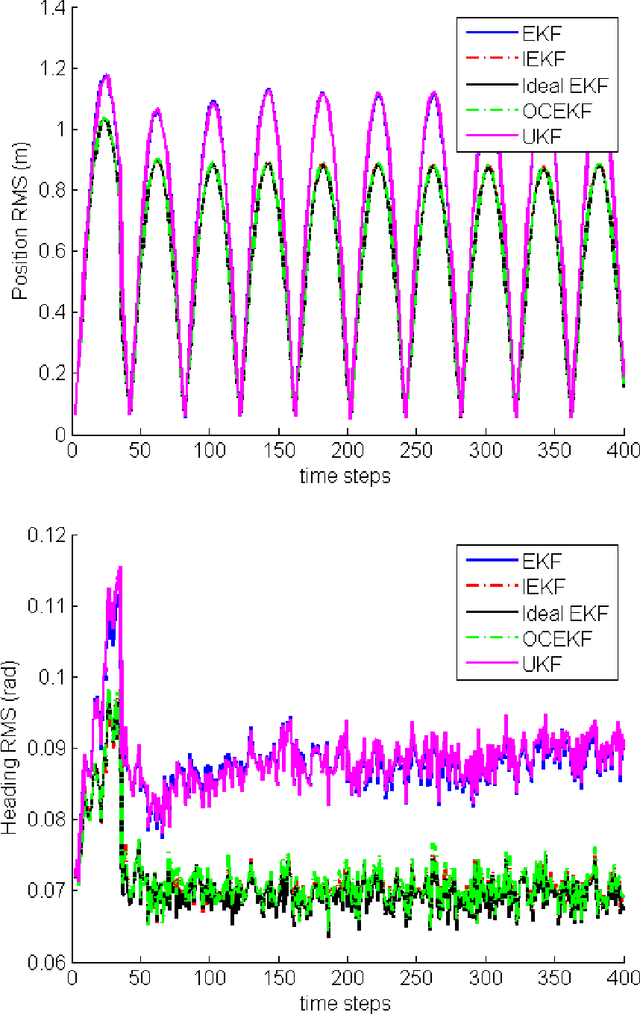
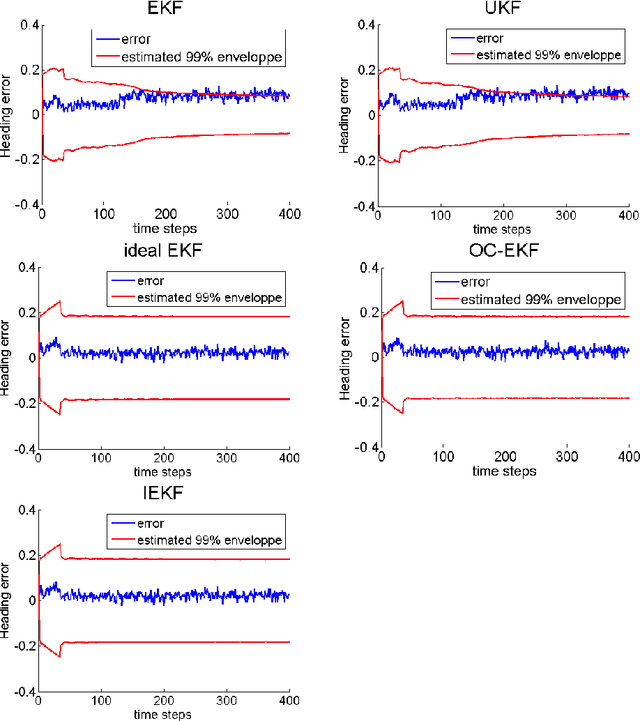
In this paper we address the inconsistency of the EKF-based SLAM algorithm that stems from non-observability of the origin and orientation of the global reference frame. We prove on the non-linear two-dimensional problem with point landmarks observed that this type of inconsistency is remedied using the Invariant EKF, a recently introduced variant ot the EKF meant to account for the symmetries of the state space. Extensive Monte-Carlo runs illustrate the theoretical results.

Intrinsic filtering on Lie groups with applications to attitude estimation

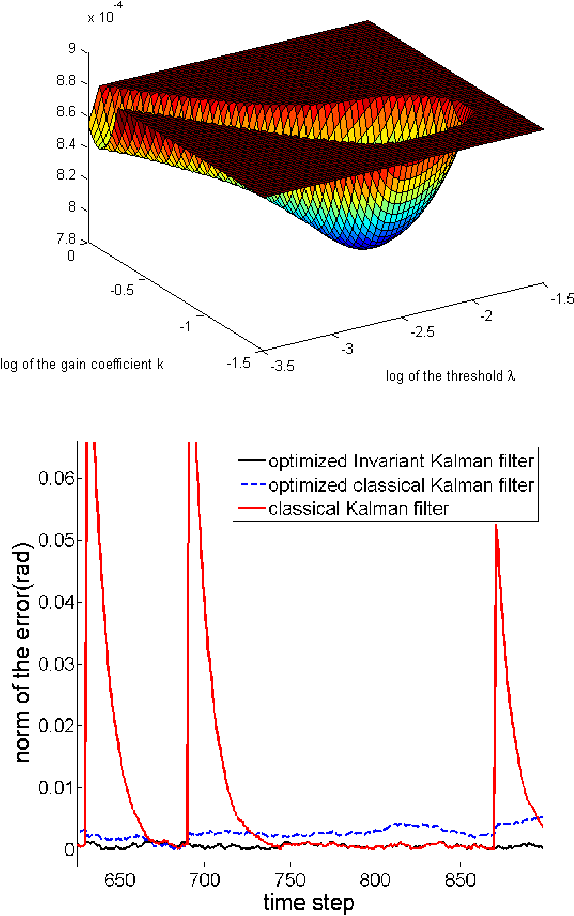
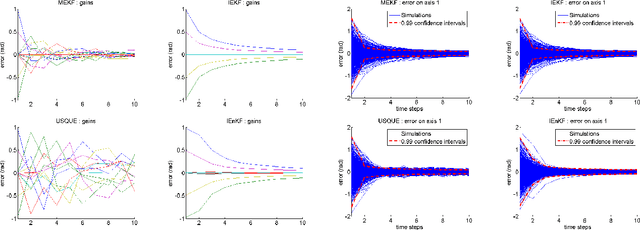
This paper proposes a probabilistic approach to the problem of intrinsic filtering of a system on a matrix Lie group with invariance properties. The problem of an invariant continuous-time model with discrete-time measurements is cast into a rigorous stochastic and geometric framework. Building upon the theory of continuous-time invariant observers, we show that, as in the linear case, the error equation is a Markov chain that does not depend on the state estimate. Thus, when the filter's gains are held fixed, and the filter admits almost-global convergence properties with noise turned off, the noisy error's distribution is proved to converge to a stationary distribution, providing insight into the mathematical theory of filtering on Lie groups. For engineering purposes we also introduce the discrete-time Invariant Extended Kalman Filter, for which the trusted covariance matrix is shown to asymptotically converge, and some numerically more involved sample-based methods as well to compute the Kalman gains. The methods are applied to attitude estimation, allowing to derive novel theoretical results in this field, and illustrated through simulations on synthetic data.

Stochastic gradient descent on Riemannian manifolds

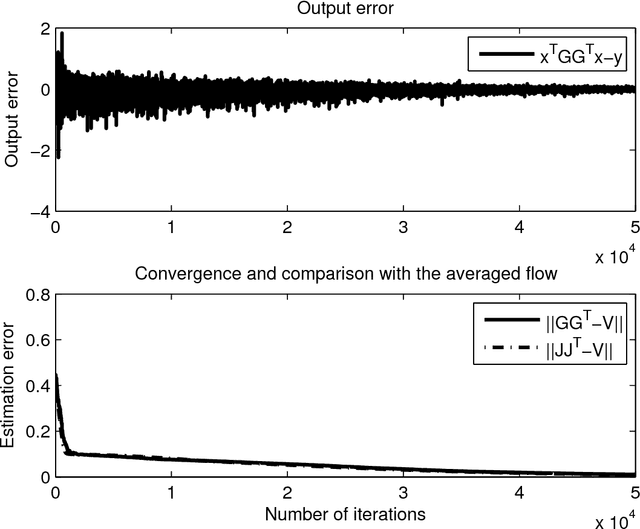
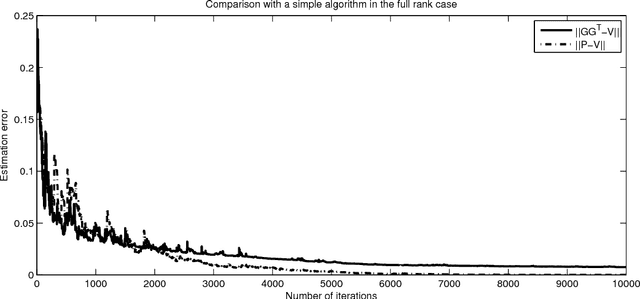
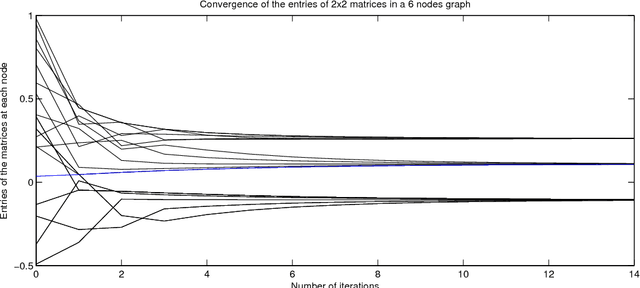
Stochastic gradient descent is a simple approach to find the local minima of a cost function whose evaluations are corrupted by noise. In this paper, we develop a procedure extending stochastic gradient descent algorithms to the case where the function is defined on a Riemannian manifold. We prove that, as in the Euclidian case, the gradient descent algorithm converges to a critical point of the cost function. The algorithm has numerous potential applications, and is illustrated here by four examples. In particular a novel gossip algorithm on the set of covariance matrices is derived and tested numerically.

Symmetries in observer design: review of some recent results and applications to EKF-based SLAM

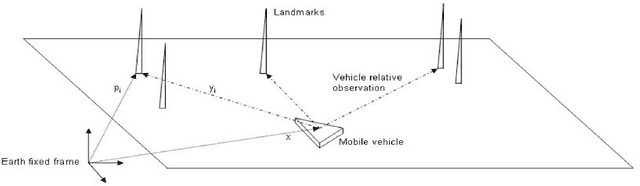
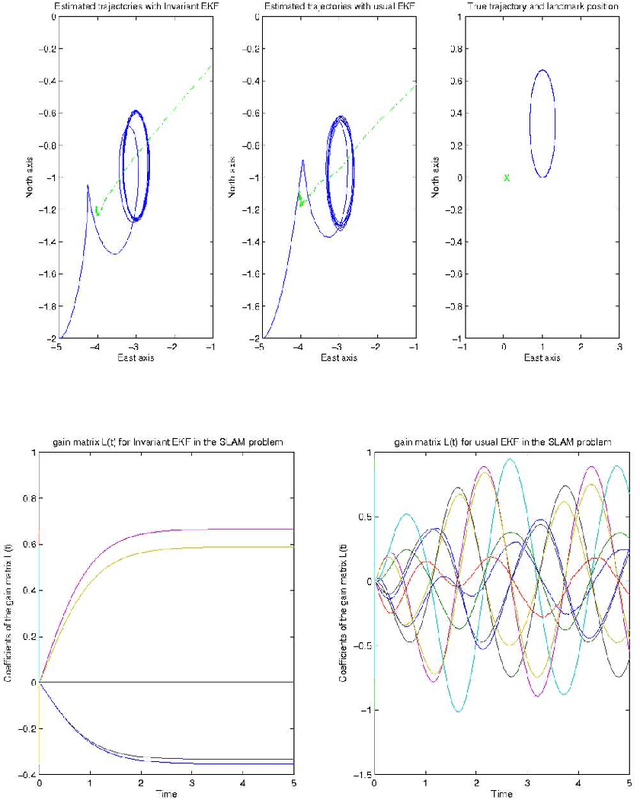
In this paper, we first review the theory of symmetry-preserving observers and we mention some recent results. Then, we apply the theory to Extended Kalman Filter-based Simultaneous Localization and Mapping (EKF SLAM). It allows to derive a new (symmetry-preserving) Extended Kalman Filter for the non-linear SLAM problem that possesses convergence properties. We also prove a special choice of the gains ensures global exponential convergence.