A Mathematical Framework for IMU Error Propagation with Applications to Preintegration
Paper and Code
Mar 09, 2020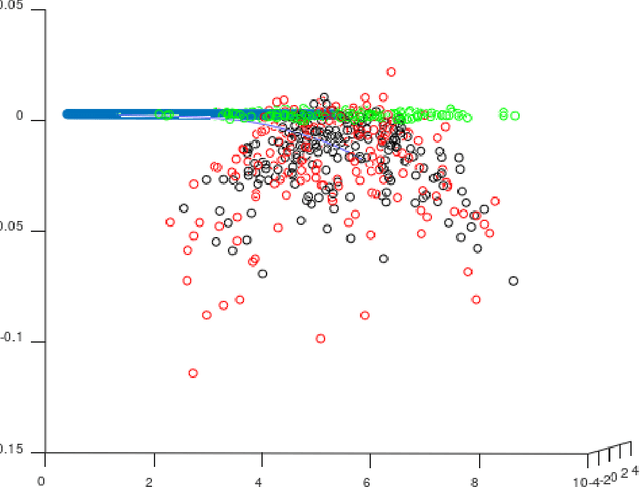
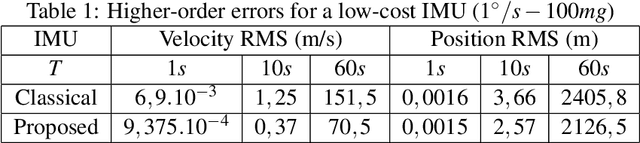
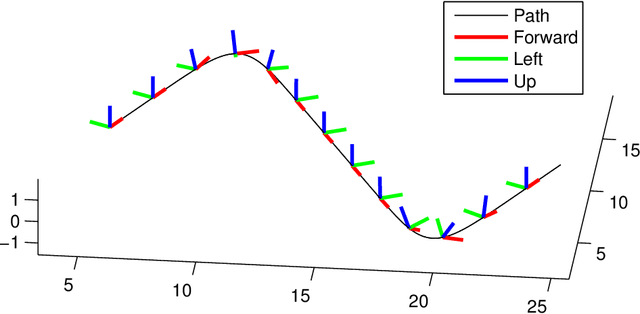
To fuse information from inertial measurement units (IMU) with other sensors one needs an accurate model for IMU error propagation in terms of position, velocity and orientation, a triplet we call extended pose. In this paper we leverage a nontrivial result, namely log-linearity of inertial navigation equations based on the recently introduced Lie group $SE_2(3)$, to transpose the recent methodology of Barfoot and Furgale for associating uncertainty with poses (position, orientation) of $SE(3)$ when using noisy wheel speeds, to the case of extended poses (position, velocity, orientation) of $SE_2(3)$ when using noisy IMUs. Besides, our approach to extended poses combined with log-linearity property allows revisiting the theory of preintegration on manifolds and reaching a further theoretic level in this field. We show exact preintegration formulas that account for rotating Earth, that is, centrifugal force and Coriolis effect, may be derived as a byproduct.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge