Intrinsic filtering on Lie groups with applications to attitude estimation
Paper and Code
Sep 12, 2014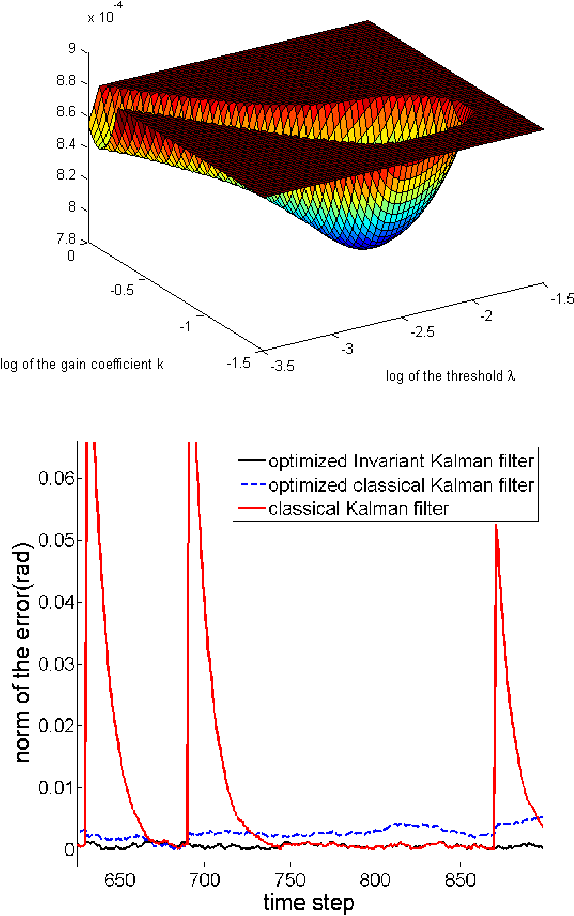


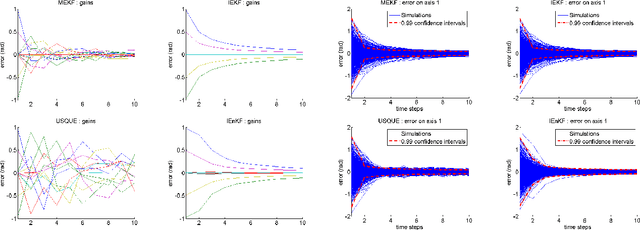
This paper proposes a probabilistic approach to the problem of intrinsic filtering of a system on a matrix Lie group with invariance properties. The problem of an invariant continuous-time model with discrete-time measurements is cast into a rigorous stochastic and geometric framework. Building upon the theory of continuous-time invariant observers, we show that, as in the linear case, the error equation is a Markov chain that does not depend on the state estimate. Thus, when the filter's gains are held fixed, and the filter admits almost-global convergence properties with noise turned off, the noisy error's distribution is proved to converge to a stationary distribution, providing insight into the mathematical theory of filtering on Lie groups. For engineering purposes we also introduce the discrete-time Invariant Extended Kalman Filter, for which the trusted covariance matrix is shown to asymptotically converge, and some numerically more involved sample-based methods as well to compute the Kalman gains. The methods are applied to attitude estimation, allowing to derive novel theoretical results in this field, and illustrated through simulations on synthetic data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge