TCLeaf-Net: a transformer-convolution framework with global-local attention for robust in-field lesion-level plant leaf disease detection

Timely and accurate detection of foliar diseases is vital for safeguarding crop growth and reducing yield losses. Yet, in real-field conditions, cluttered backgrounds, domain shifts, and limited lesion-level datasets hinder robust modeling. To address these challenges, we release Daylily-Leaf, a paired lesion-level dataset comprising 1,746 RGB images and 7,839 lesions captured under both ideal and in-field conditions, and propose TCLeaf-Net, a transformer-convolution hybrid detector optimized for real-field use. TCLeaf-Net is designed to tackle three major challenges. To mitigate interference from complex backgrounds, the transformer-convolution module (TCM) couples global context with locality-preserving convolution to suppress non-leaf regions. To reduce information loss during downsampling, the raw-scale feature recalling and sampling (RSFRS) block combines bilinear resampling and convolution to preserve fine spatial detail. To handle variations in lesion scale and feature shifts, the deformable alignment block with FPN (DFPN) employs offset-based alignment and multi-receptive-field perception to strengthen multi-scale fusion. Experimental results show that on the in-field split of the Daylily-Leaf dataset, TCLeaf-Net improves mAP@50 by 5.4 percentage points over the baseline model, reaching 78.2\%, while reducing computation by 7.5 GFLOPs and GPU memory usage by 8.7\%. Moreover, the model outperforms recent YOLO and RT-DETR series in both precision and recall, and demonstrates strong performance on the PlantDoc, Tomato-Leaf, and Rice-Leaf datasets, validating its robustness and generalizability to other plant disease detection scenarios.

Tool or Tutor? Experimental evidence from AI deployment in cancer diagnosis

Professionals increasingly use Artificial Intelligence (AI) to enhance their capabilities and assist with task execution. While prior research has examined these uses separately, their potential interaction remains underexplored. We propose that AI-driven training (tutor effect) and AI-assisted task completion (tool effect) can be complementary and test this hypothesis in the context of lung cancer diagnosis. In a field experiment with 334 medical students, we manipulated AI deployment in training, in practice, and in both. Our findings reveal that while AI-integrated training and AI assistance independently improved diagnostic performance, their combination yielded the highest accuracy. These results underscore AI's dual role in enhancing human performance through both learning and real-time support, offering insights into AI deployment in professional settings where human expertise remains essential.

Novel tile segmentation scheme for omnidirectional video

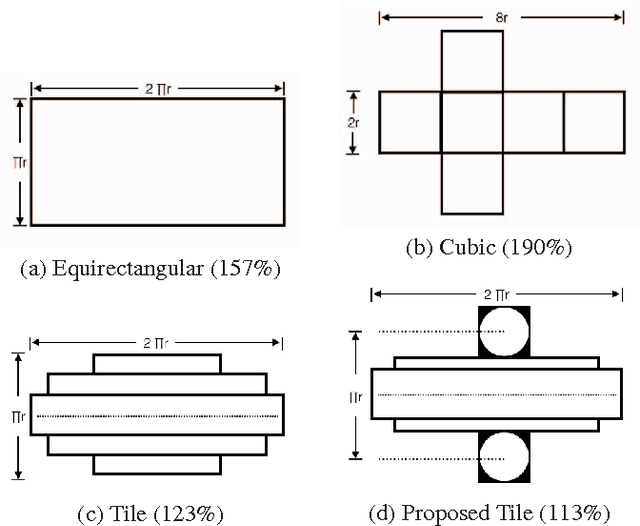
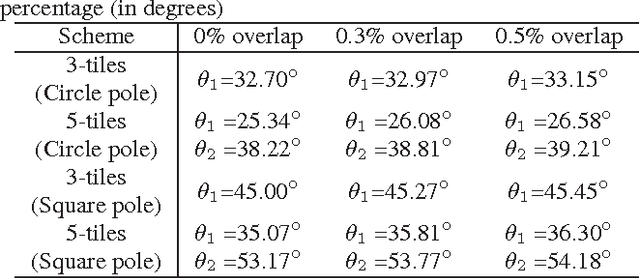
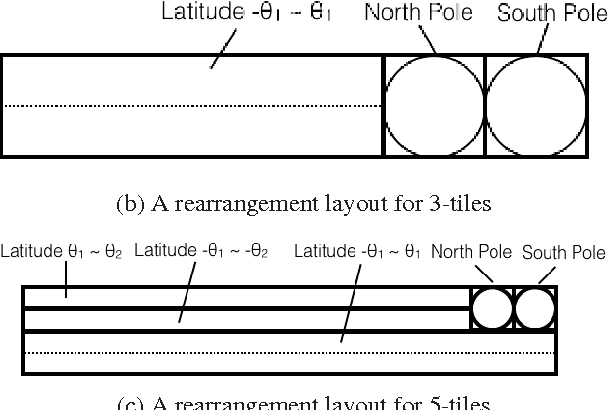
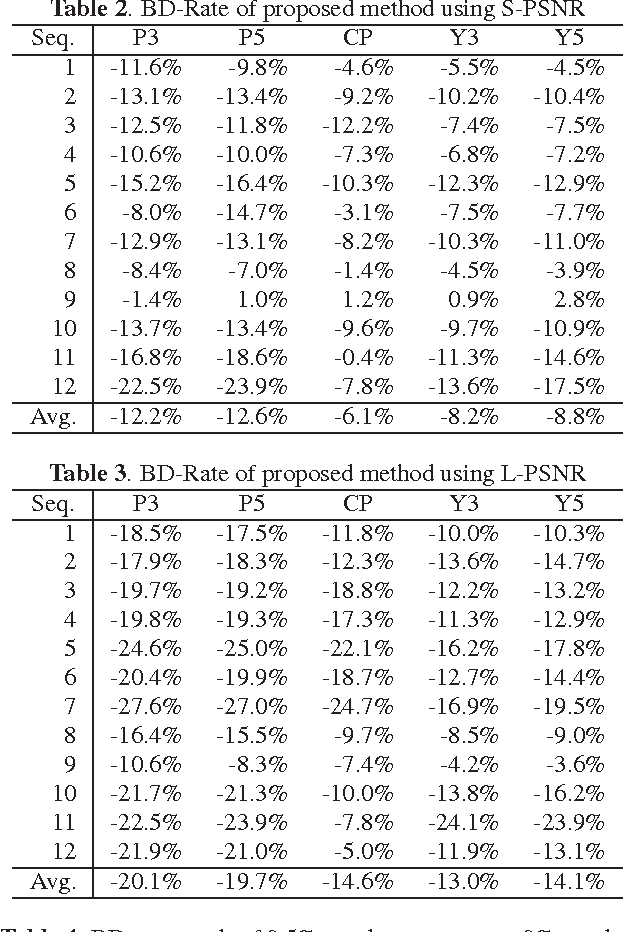
Regular omnidirectional video encoding technics use map projection to flatten a scene from a spherical shape into one or several 2D shapes. Common projection methods including equirectangular and cubic projection have varying levels of interpolation that create a large number of non-information-carrying pixels that lead to wasted bitrate. In this paper, we propose a tile based omnidirectional video segmentation scheme which can save up to 28% of pixel area and 20% of BD-rate averagely compared to the traditional equirectangular projection based approach.

Demystifying ResNet

The Residual Network (ResNet), proposed in He et al. (2015), utilized shortcut connections to significantly reduce the difficulty of training, which resulted in great performance boosts in terms of both training and generalization error. It was empirically observed in He et al. (2015) that stacking more layers of residual blocks with shortcut 2 results in smaller training error, while it is not true for shortcut of length 1 or 3. We provide a theoretical explanation for the uniqueness of shortcut 2. We show that with or without nonlinearities, by adding shortcuts that have depth two, the condition number of the Hessian of the loss function at the zero initial point is depth-invariant, which makes training very deep models no more difficult than shallow ones. Shortcuts of higher depth result in an extremely flat (high-order) stationary point initially, from which the optimization algorithm is hard to escape. The shortcut 1, however, is essentially equivalent to no shortcuts, which has a condition number exploding to infinity as the number of layers grows. We further argue that as the number of layers tends to infinity, it suffices to only look at the loss function at the zero initial point. Extensive experiments are provided accompanying our theoretical results. We show that initializing the network to small weights with shortcut 2 achieves significantly better results than random Gaussian (Xavier) initialization, orthogonal initialization, and shortcuts of deeper depth, from various perspectives ranging from final loss, learning dynamics and stability, to the behavior of the Hessian along the learning process.