Siddharth Soni
A Neural Network-Based Search for Unmodeled Transients in LIGO-Virgo-KAGRA's Third Observing Run
Dec 27, 2024



Abstract:This paper presents the results of a Neural Network (NN)-based search for short-duration gravitational-wave transients in data from the third observing run of LIGO, Virgo, and KAGRA. The search targets unmodeled transients with durations of milliseconds to a few seconds in the 30-1500 Hz frequency band, without assumptions about the incoming signal direction, polarization, or morphology. Using the Gravitational Wave Anomalous Knowledge (GWAK) method, three compact binary coalescences (CBCs) identified by existing pipelines are successfully detected, along with a range of detector glitches. The algorithm constructs a low-dimensional embedded space to capture the physical features of signals, enabling the detection of CBCs, detector glitches, and unmodeled transients. This study demonstrates GWAK's ability to enhance gravitational-wave searches beyond the limits of existing pipelines, laying the groundwork for future detection strategies.
Merged-GHCIDR: Geometrical Approach to Reduce Image Data
Sep 06, 2022
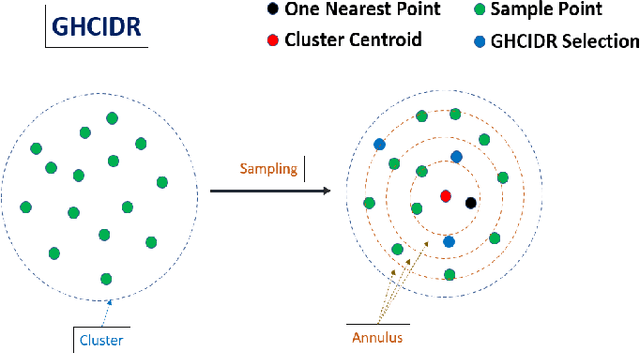
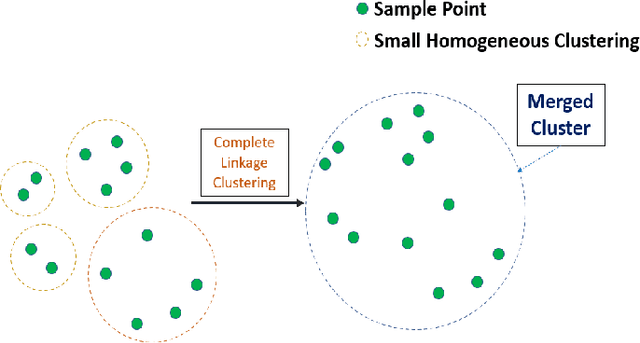
Abstract:The computational resources required to train a model have been increasing since the inception of deep networks. Training neural networks on massive datasets have become a challenging and time-consuming task. So, there arises a need to reduce the dataset without compromising the accuracy. In this paper, we present novel variations of an earlier approach called reduction through homogeneous clustering for reducing dataset size. The proposed methods are based on the idea of partitioning the dataset into homogeneous clusters and selecting images that contribute significantly to the accuracy. We propose two variations: Geometrical Homogeneous Clustering for Image Data Reduction (GHCIDR) and Merged-GHCIDR upon the baseline algorithm - Reduction through Homogeneous Clustering (RHC) to achieve better accuracy and training time. The intuition behind GHCIDR involves selecting data points by cluster weights and geometrical distribution of the training set. Merged-GHCIDR involves merging clusters having the same labels using complete linkage clustering. We used three deep learning models- Fully Connected Networks (FCN), VGG1, and VGG16. We experimented with the two variants on four datasets- MNIST, CIFAR10, Fashion-MNIST, and Tiny-Imagenet. Merged-GHCIDR with the same percentage reduction as RHC showed an increase of 2.8%, 8.9%, 7.6% and 3.5% accuracy on MNIST, Fashion-MNIST, CIFAR10, and Tiny-Imagenet, respectively.
Geometrical Homogeneous Clustering for Image Data Reduction
Aug 27, 2022
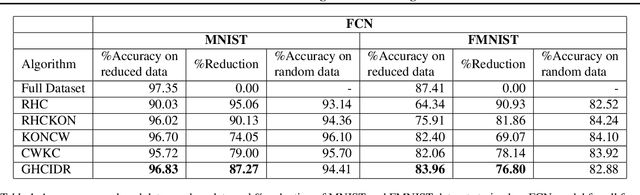
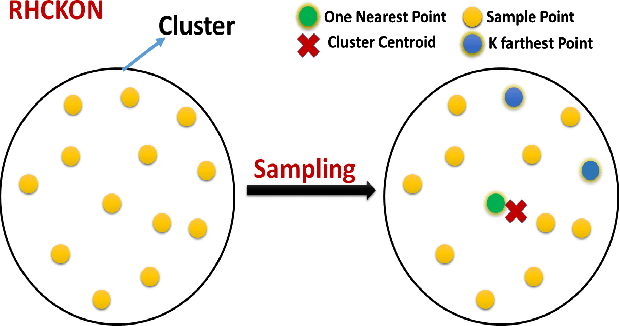
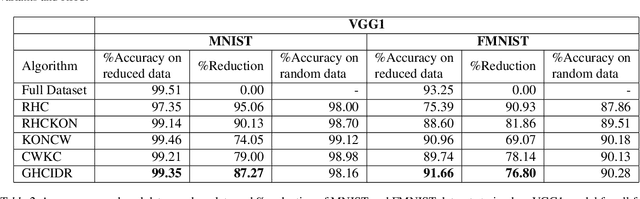
Abstract:In this paper, we present novel variations of an earlier approach called homogeneous clustering algorithm for reducing dataset size. The intuition behind the approaches proposed in this paper is to partition the dataset into homogeneous clusters and select some images which contribute significantly to the accuracy. Selected images are the proper subset of the training data and thus are human-readable. We propose four variations upon the baseline algorithm-RHC. The intuition behind the first approach, RHCKON, is that the boundary points contribute significantly towards the representation of clusters. It involves selecting k farthest and one nearest neighbour of the centroid of the clusters. In the following two approaches (KONCW and CWKC), we introduce the concept of cluster weights. They are based on the fact that larger clusters contribute more than smaller sized clusters. The final variation is GHCIDR which selects points based on the geometrical aspect of data distribution. We performed the experiments on two deep learning models- Fully Connected Networks (FCN) and VGG1. We experimented with the four variants on three datasets- MNIST, CIFAR10, and Fashion-MNIST. We found that GHCIDR gave the best accuracy of 99.35%, 81.10%, and 91.66% and a training data reduction of 87.27%, 32.34%, and 76.80% on MNIST, CIFAR10, and Fashion-MNIST respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge